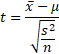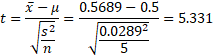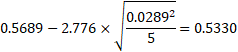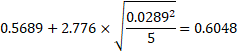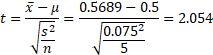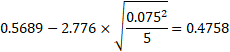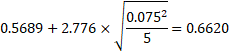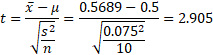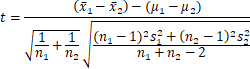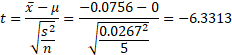第1回（SUNATEC e-Magazine　vol.147）では、母集団の性質と標本の関係を解説した。
無作為に選んだ標本は、母集団と以下のような関係がある。
・正規分布する母集団から無作為に抽出した標本の平均値（標本平均）の
　　　　　期待値は母集団の平均値（母平均）μ　に等しい
　　　　　分散は母集団の分散（母分散）σ²の1/nに等しい
　正規分布する母集団から無作為に抽出した標本の分散（標本分散）s²の
　　　　　期待値は母分散σ²に等しい
・平均 μ 、分散σ²の任意の母集団（正規分布でなくてもよい）から、大きさnの標本を無作為に抽出して得られ
　る確率変数の平均は、nを十分大きくとるとμに近づく。（大数の法則）
・平均 μ 、分散σ²の任意の母集団から、大きさnの標本を無作為に抽出して得られる標本平均の分布は、nが
　大きくなるにつれて、平均 μ 、分散σ²/ nの正規分布に近づく。（中心極限定理）
・事象Eが出現する確率pが定まった母集団から、大きさnの標本を抽出するとき、n回中x回に事象Eが起こる
　確率は、二項分布に従い、その期待値はnp、分散はnp（1-p）である。

第2回では、以上の母集団の性質と標本の関係から、母平均を推定・検定する方法を解説する。

多くの状況では、母平均 μや母分散 σ²は未知であり、標本平均 や標本分散s²が観測できる値である。これらの観測できる標本のパラメータから、母集団の未知のパラメータを見つもる方法が推定である。

前提として、母集団は正規分布しているとする。正規分布する母集団から無作為に抽出した標本の平均（標本平均）の
　　　　　期待値は母平均 μに等しい
という関係から、標本平均は母平均の不偏推定値である。標本は選ぶごとに変わるので、とμは、必ず一致しているわけではないが、全く無関係ではなく、はμの周辺に存在する。
　　　　　分散は母集団の分散（母分散）σ²の1/nに等しい
ことから、大きな標本（nが大きい）になれば、1/nは小さくなって、標本平均の分散が小さくなり、その結果の存在する範囲はμに近くなっていく。従って、の存在する範囲を知るには、母集団の分散σ²も推定しなければならない。
　第1回で、正規分布する母集団から無作為に抽出した標本の分散（標本分散）s²の期待値は母分散σ²に等しいことを示した。このため、標本分散は母分散の不偏推定値である。しかし、標本分散の平方根である標本標準偏差sの期待値は、母標準偏差σとは一致しない。sの期待値とσの比は、n=3では0.8862、n=5では0.9400、n=10では0.9727で、nが大きくなるにつれて、sの期待値とσは近づいていき、最後には一致する。標本分散と母分散の比の分布は　に従う。nが小さいときのの広がりは大きく、nが大きくなると次第に小さくなる。標本分散の分布については、第3回で詳細に解説する。
　大標本であれば標本分散s²は母分散σ²とほぼ等しいと期待されるので、標本平均 は母平均 μを平均とする正規分布に従って分布し、その標準偏差はとなる。第1回に示した標準正規分布確率密度の図から分かるように、中心から±2×標準偏差の範囲に全体の95.45 ％が含まれる。これは95％よりわずかに大きい。95%が含まれる範囲は、中心から±1.960 × 標準偏差の範囲となる。従って、μの95％信頼区間は、 の範囲となる。

例　採取した100試料中の物質Aの濃度を測定したところ、100個の測定結果の平均値（標本平均）が0.0254 mg/kg、標準偏差（標本標準偏差）が0.0067 mg/kgであった。このとき母平均の95％区間は
  から　
となる。
　一方、測定値を（上の例では0.0254±0.0067）のように表すことがある。これはデータ全体（あるいは母集団に含まれる値全体）の範囲を平均値と標準偏差で表している。データを見たり、示したりする時には、測定値の範囲なのか（母）平均の信頼区間なのかを明確に区別する必要がある。

これまでの解説は大標本の場合であるが、標本の数が少ない小標本では、成立しない仮定がある。大標本であれば標本分散s²は母分散σ²とほぼ等しいと期待されるが、小標本では標本分散が広い範囲に分布するので、標本平均の分布の標準偏差がであるとは言えなくなる。従って、95％信頼区間も、95％の確率で母平均を含むとは言えなくなる。それで、小標本において母平均を推定するために、t（Student‘s t）という統計量が使われる。

tは自由度n-1のt分布 に従う。tが

の範囲にある確率は95％である。この式を変形すると

となり、これが母平均の95％信頼区間となる。大標本の場合と比較すると、の係数が変わっている。大標本では正規分布の95％範囲である1.960だが、小標本ではその大きさ（n）に対応したt分布の値が使われる。nが小さいときのt分布の形は、中央付近の確率密度が小さく左右に広がっている。そのため、95％が含まれる範囲は、正規分布よりも広くなる。この値は、t分布表で得ることができる。n =100の場合は、自由度がn -1＝99となるので、t分布表から自由度99の値を読み取ると、t（99,0.05）=1.984となり、正規分布の場合の1.960よりわずかに大きいが、1％程度の違いなので実用的には問題ない。n=5の小標本ではt（4,0.05）=2.776となり、正規分布の1.960よりもかなり大きくなる。
例　採取した5試料中の物質Aの濃度を測定したところ、5個の測定結果の平均値（標本平均）が0.0254 mg/kg、標準偏差（標本標準偏差）が0.0067 mg/kgであった。このとき母平均の95％信頼区間は、t（4,0.05）=2.776を用いて
  から　
となる。大標本の場合（0.0241～0.0267）と比較すると、小標本による母平均推定値の95％区間は非常に広いことが分かる。測定値を0.0254±0.067と表すだけなら、標本の大きさは影響がないが、母数の推定では標本の大きさは非常に重要である。

検定は、母集団の性質（割合、平均、標準偏差）に仮説を立て、標本の値に基づいて真偽を決定することである。第1回の統計的推論の例で示した、「ある測定の結果が10以上である確率は0.9である」という仮説を、実際の測定により否定したのは、割合の検定の一例である。

母平均の検定

基準になる値（成分量の下限値、農薬濃度の上限値など）があって、試料を測定した平均と基準になる値を比較することは、よく行われている。これは、実際には母平均の検定を行っているが、必ずしも意識されていないし、正しく行われていないことも多い。
　ある製品中の物質の上限値（基準になる値）が0.5であり、ロットの平均がこれを超過すれば不適合、これ以下であれば適合であるとする。ロットを試験したときの測定値が、0.6147、0.5586、0.5786、0.5502、0.5425であった時、平均値（標本平均）は0.5689、標準偏差（標本標準偏差）は0.0289と計算される。仮説は、「母平均は0.5である。」とする。推定の項で示したように、標本からtを計算する。

n=5、P=0.05、のt 値は2.776であり、計算したt値はこれよりも大きい。従って、「母平均は0.5である。」は否定され、母平均は0.5ではないことになる。母平均の信頼区間を計算すると

となり、母平均の信頼区間内に0.5が含まれていない。
　別のロットを試験したときの測定値の平均値（5回測定）が同様に0.5689で、標準偏差（標本標準偏差）は0.075であったとする。標本からtを計算すると、

となり、「母平均は0.5である。」は否定されない。つまり、このロットが基準に適合していないとは言えなくなってしまう。このときの母平均の信頼区間を計算すると

となり、信頼区間内に0.5が含まれている。
　仮に、10回の測定の結果から同じ標本平均と標本標準偏差が得られたなら、

となり、「母平均は0.5である。」という仮説は否定される。

平均の差の検定

平均の差の検定は、2つの標本が同じ母集団から得られたかどうかを検定する。この時の帰無仮説は、「2つの標本が採られた母集団の母平均は等しい。」である。
　2つの測定方法で同じ試料を測定したとき、平均が一致するとは限らない。しかし、同一の測定法であっても一致するわけではないから、2つの測定が同じ結果を与えているかは、検定をして調べる必要がある。この検定のために、平均値の差の検定が使われる。平均の差の検定もtを使って行われるが、対応のない又は対になっていない（unpaired）検定と対応のある又は対になった（paired）検定の2種類がある。
　2つの検定の違いを、分析条件を比較する例で説明する。2つの条件で試料を分析し、得られた結果に差があるかを知りたいとする、この時、1つの試料から採取した試験試料を2つの条件で繰り返し測定する実験計画（計画１）と、異なる試料をそれぞれ2つの条件で測定する実験計画（計画２）があり得る。
　計画１では
条件１　　平均＝0.52596、標準偏差＝0.0479　　5回測定
条件２　　平均＝0.40718、標準偏差＝0.0617　　7回測定
のようなデータが得られる。
　計画２では
　　　　　　条件１　　　　条件２　　　　
試料１　　0.254　　　　　0.325
試料２　　1.345　　　　　1.458
試料３　　0.658　　　　　0.701
試料４　　1.253　　　　　1.315
試料５　　0.474　　　　　0.563
のようなデータが得られる。計画1では2つの条件の1番目のデータ間に特に関係はなく、2条件のデータ数が等しい必要もない。計画2では条件１と2の1番目の結果、2番目の結果には同じ試料から得られたという関連があり、2つの条件のデータの数は等しい。計画１では対応のないt検定が、後の例では対応のあるt検定が行われる。
　最初に対応のないt検定について解説する。平均値の差のt検定で想定する母集団は、その試料から条件１で得られるであろう結果の集合（平均μ1）と条件２で得られるであろう結果の集合（平均μ2）である。2つの集合の平均値が等しいか（実際には分散も等しいと仮定するので、同じ母集団であるか）を検定するため、帰無仮説は　μ1＝μ2　あるいは　μ1 - μ2＝0である。
　平均がμ1とμ2の2つの確率変数の差の期待値は、μ1 - μ2＝0　である。両者の母分散が等しいとすれば、差の母分散は

で推定され、標本のtは

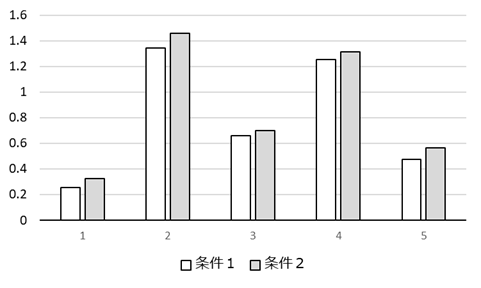
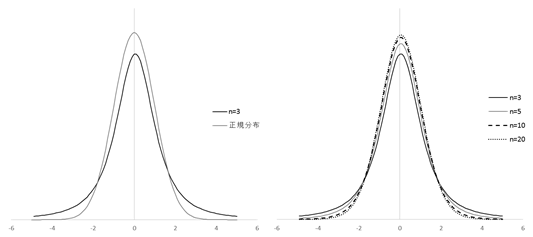
で計算される。仮説から　μ1＝μ2なので、tは3.585になる。自由度は5+7-2＝10であり、t(10,0.05)＝2.228である。標本から求めたt値（3.585）はこれより大きいため仮説　μ1＝μ2は否定され、条件１と条件２の結果の平均値は等しいとは言えないと結論される。

計画２では、条件１の平均値は0.7968、標準偏差は0.2317、条件２の平均値は0.8724、標準偏差は0.2409である。このデータに、上記で説明した対応のないデータの平均値の差の検定を行うと、t＝0.2459であり、t（8, 0.05）=2.306よりも小さいので、「平均値は等しい。」という仮説は否定されない。しかし、データをグラフにしてみると分かるように、常に条件2の方が大きな値を与えている。

それなのに、検定で2つの平均値が等しいという仮説が否定されないのは、差の分散にそれぞれの試料の濃度の変動が含まれたため、tの計算式の分母が大きくなってしまったからである。このような場合には、対応のあるデータの差dの母平均が0であるかを検定する。帰無仮説はd=0である。
　計画2のデータで、条件1の結果から条件2の結果を引いた差は、-0.071、-0.113、-0.043、-0.062、-0.089となる。平均は-0.0756、標準偏差sは0.0267である。データ数は差の数なので、n=5である。母平均の検定で示したようにtを求めると。

となる。負の価のtが得られるが、差の計算を逆にすればtは6.3362となる。自由度は4なので、t（4, 0.05）=2.776と比較すると、得られたtの方が大きくなり、帰無仮説d=0が否定される。この結果、条件1と条件2の結果には差があるという結論が得られる。

検定では、まず検定する内容を否定する仮説をたてる。この仮説を、帰無仮説あるいはゼロ仮説と呼ぶ。上の例では、「母平均は0.5である。」あるいは「差の平均は0である。」が帰無仮説となる。
　次に、その仮説が正しい場合に起こる事象の範囲を定める。上の例では、その仮説が正しければ、標本から計算したtが、自由度と確率で定まるtより小さくなるはずである。
　測定結果が、その範囲に入るかどうかを調べる。
　もし、範囲に含まれないならば、帰無仮説は否定され、含まれるなら帰無仮説は否定されない。ここで注意すべきは、否定されなかったからと言って、帰無仮説が正しいとはならないことである。正確に言うなら、帰無仮説を否定する十分な根拠がないということになる。たとえば、測定数を多くすれば、標本平均と標本標準偏差が同じでも、tが大きくなるので、検定の結果は変わる可能性がある。つまり、帰無仮説は否定されたときにはじめて意味を持つ。
　従って、2つの平均値が等しい、2つの実験条件は同等の結果を与える、といったことの証明のために平均値の差を使うことはあまり適切ではない。帰無仮説が否定されないようにするためには、tを小さくすれば良いので、分母にあるが大きい実験ではtが小さくなる。つまり、バラつきが大きい実験を少ない回数行えば、有意の差はなくなるが、これは適切な実験結果に基づいた検定とはいえない。
　帰無仮説として「母平均は0.5ではない。」という仮説を用いると、これを否定して母平均が0.5である検定ができそうに思えるかもしれない。しかし、母平均が0.5ではないとすると、母平均として想定される値は無数にあり、仮説が正しい場合に起こる事象の範囲を定める（つまりtを求める）ことができないので、検定が不可能になる。

検定では、帰無仮説が正しい場合に起こる事象の範囲を定め、それと実際に得られた結果を比較する。得られる結論は、
・得られた結果は、事象の範囲外である。→帰無仮説が否定される。
・得られた結果は、事象の範囲内である。→帰無仮説が否定されない。
の2つである。しかし、帰無仮説が正しい場合に起こる事象の範囲を定める時に、何%が含まれるかを考慮している。これが危険率であり、t（4, 0.05）の0.05が確率を示している。つまり、帰無仮説が正しいとしても、範囲外になる確率が5％ある。危険率を1％にすると区間が広がる（tが大きくなる）ので、区間外になる確率は1％になる。ただし、区間は非常に広くなるので、帰無仮説が正しくないのに、範囲内に入ってしまい、否定されなくなる確率は大きくなる。
　統計ソフトでは、「P（T<=t）両側」のような形で確率が示されている。これは、そのt値が得られたときに、帰無仮説が正しい確率を示している。例えば、計画２の例を統計ソフトで解析すると、「P（T<=t）両側」は0.0032つまり0.3％である。このことは、2つの条件の差が0であるときに、2つの結果がこの程度の差になる確率は、0.3％しかないと解釈される。

　推定値の期待値が母数に等しいとき、その推定値は不偏推定値である。不偏推定値が複数あるとき、それらの中で分散が最小のものが、最良不偏推定値である。

（戻る）

　「95％信頼区間中に母平均μが含まれる確率は95％である。」と説明されることが多い。
この文章をよく読むと、疑問が起こる。ある標本からは1つの標本平均と１つ標本分散が求められるので、信頼区間が1つだけ定まる。一方、母平均μは未知ではあるが、分布しない単一の値である。単一の値は、ある区間に含まれるか含まれないかのどちらかであって、確率を求めることはできない。では、95％という確率は何を意味しているか？
　この文章の意味は、標本抽出を繰り返したときに求められる多数の信頼区間の95％は母平均μを含むということである。母平均が分布していて、その95％が信頼区間に含まれるわけではない。

（戻る）

　下の図の左は自由度2のt分布と正規分布を示している。t分布は正規分布に比べて、中央の確率密度は小さく、両端の広がりは大きい。右は、自由度が異なるt分布を示す。自由度が大きくなると、t分布は正規分布に近づく。

（戻る）

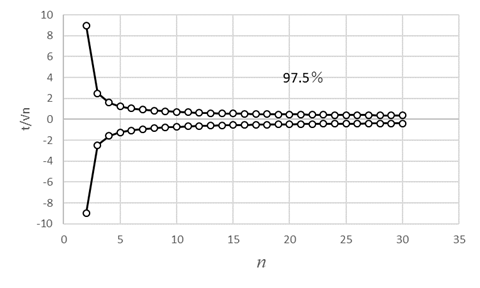
において、標準偏差sの係数であると　のnによる変化を下図に示す。

標本の大きさnが大きくなるとともに、　は小さくなる。つまり推定の信頼性が向上する。nが3の時には　は0.68である。3回の繰り返しで平均を求めると、真の標準偏差の1/5から2倍程度の値になり、正しく推定できるとは言い難い。

（戻る）

松田　りえ子（まつだ　りえこ）

1977年　京都大学大学院薬学研究科修士課程終了
1977年　国立衛生試験所薬品部入所
1990年　国立医薬品食品衛生研究所　食品部　主任研究官
2000年　同　食品部　第二室長
2003年　同　食品部　第四室長
2007年　同　食品部　第三室長
2008年　同　食品部長
2013年　同　退職　（再任用）
2017年　同　安全情報部客員研究員、公益社団法人食品衛生協会技術参与