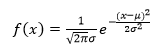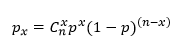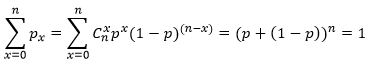|
分析者が知っていて欲しい統計
国立医薬品食品衛生研究所 安全情報部
客員研究員(元食品部長) 松田 りえ子 「分析者が知っていて欲しい統計」は5回のシリーズで、次のような内容を扱う。 第1回 母集団と標本統計は何をしているか第1回では、母集団の性質と標本の関係を解説する。一般的に、統計はある集団を観察しその性質を数量的に記述する手法である。もっとも簡単なのは、その集団の代表値(平均値)や割合を求めること(集計)である。これはニュース等で最もよく目にするもので、学力テストの平均値や、〇〇に賛成か反対かのアンケート結果等はよく報道されている。次に、集計の結果から集団に関する推測や判断を行うにも統計が用いられる。この作業は推定、推計、推論、予測と呼ばれる。上の例に挙げたアンケートの結果は、対象者全員ではなく一部の人に実施した結果から、全体の割合を推定している。逆に、推測(仮説)が先にあり、それが合理的かどうかを検証するにも統計が用いられる。これは仮説検定である。 母集団統計が推定や仮説検定をするときの基礎の基礎は、母集団の特定である。最初にどの集団に対して統計を適用するかを明らかにしておかないと、標本の取り出し(サンプリング)が不適切になり、統計の理論を適用することができなくなる。 Q 以下の調査で想定している母集団と特性は何か? 1. 世論調査 (〇〇についてどう考えますか?) 調査を始める前に、最終的にどのような特性を集計するかを考えて、必要な調査(分析)項目をあらかじめ決めておく必要がある。店頭買い上げ魚のダイオキシン濃度調査において、最終的に魚の大きさが必要となっても、分析後に試料はないので、大きさの調査は不可能である。魚の大きさとダイオキシン類濃度の関係が知りたければ、もう一度調査するしかない。 標本母集団が大きい場合、全ての構成要素を調査することは不可能(あるいは困難)なため、母集団を代表する一部分である標本の観察を行うのが一般的である。なぜ標本から母集団の特性を推論できるのか? それは、無作為に選んだ標本は、母集団と確率で結ばれているからである。逆に言えば、標本が母集団から無作為に選ばれていなければ、標本の特性から母集団の特性を予想することはできない。このような無作為標本を選ぶ方法がサンプリングである。サンプリングについては第4回で解説する。 統計的推論標本が無作為に選ばれているという前提で、統計的推論の手順を示す。これは特性がattributeの場合である。 このためには、標本の性質と母集団の性質を結びつける、確率の定理が必要である。 統計的推論の例を示す。 1.仮説:ある測定の結果が10以上である確率は0.9である。 2.測定を5回くり返したとき、5個の結果はどれも10を超えなかった。「10を超えない」は、10以上の排反事象なので、「測定の結果が10以上である確率は0.9である。」という仮説が正しければ、「10を超えない」確率は(1-0.9=0.1)である。5回の測定は独立とし、結果A-Eが得られたとする。A-Eが「10を超えない」確率は0.1であり、乗法定理より5回とも10を超えない確率は 3.「測定を5回くり返したとき、結果は10を超えない」という結果が得られる確率は非常に低いので、「測定の結果が10以上である確率は0.9である。」という仮説は誤りと結論する。 標本の分布構成要素の数が50の有限母集団から、5つの構成要素を選んで標本とする。このときに、構成要素が区別できるなら、標本の数は 特性がattributeである分布からの標本の分布は、二項分布で記述される。 n=5、pが0.9の二項分布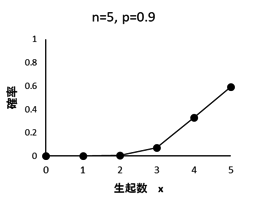 特性がvariableである分布からの標本の分布は母集団の分布によって変わるが、正規分布する母集団から採られた標本の性質はよくわかっている。 正規分布する母集団から無作為に抽出した標本の平均(標本平均) 下図に平均が50で標準偏差が10(分散が100)の母集団からn=5の標本を100個抽出したときの、標本平均と標本標準偏差の分布を示す。〇は母平均である50の周囲に分布している。上に示した性質から、標本平均値の95%は41-59の範囲に分布すると予想され、この例で41-59に入った数は47個であった。n=100の標本の平均値の95%は48-52の範囲に分布する。n=100の標本の平均値の範囲はn=5の場合に比較してとても狭く、1つの標本の平均値であっても信頼性が高いといえる。 平均が50で標準偏差が10(分散が100)の母集団から抜き取ったn=5の標本平均の分布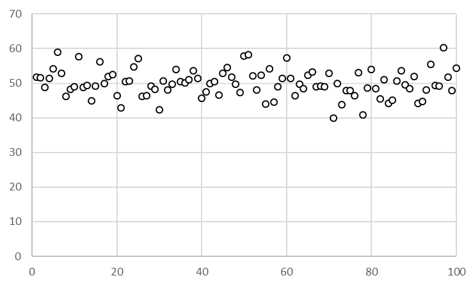 一方、n=5の標本の標本標準偏差は下図のような分布を示す。母集団の標準偏差は10であるが、最も小さい標本標準偏差は1.4、最も大きいものは17.3であった。このように標本標準偏差は標本平均に比較して、特に小標本の場合には分布が広くなる。 平均が50で標準偏差が10(分散が100)の母集団から抜き取ったn=5の標本標準偏差の分布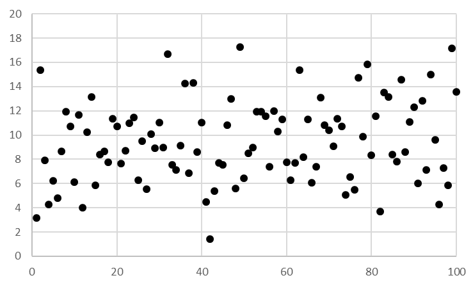 また、大数の法則 平均 μ 、分散σ2の任意の母集団(正規分布でなくてもよい)から、大きさnの標本を無作為に抽出して得られる確率変数の平均は、nを十分大きくとるとμに近づく。 中心極限定理 平均 μ 、分散σ2の任意の母集団から、大きさnの標本を無作為に抽出して得られる標本平均の分布は、nが大きくなるにつれて、平均 μ 、分散σ2/ nの正規分布に近づく。 により、母集団の分布によらず、無作為に抽出した標本の平均及び分散と、母平均及び母分散が関係づけられている。ここで、無作為に抽出した標本であることと、標本の大きさnが重要である。無作為ではない標本の特性と母集団の特性を結びつけるものは何もないので、本来の目的である母集団の特性については何もわからない。 今回は母集団の性質が明らかな時の、標本平均、標本標準偏差の分布を説明した。しかし、実際には得られるのは標本であり、それから母集団を推定することが多い。第2回は標本が得られたときに、母集団の性質を推定する方法を解説する。 世論調査 (戻る) 国民健康栄養調査 (戻る) 魚中のダイオキシン類の濃度調査(店頭買い上げ) (戻る) 燻製食品中のPAH濃度調査(燻製を製造して調査) (戻る) 清涼飲料水中の重金属の分析法の性能評価 (戻る) 確率の定理 事象 A の余事象 事象 A と B の少なくともどちらかが起こる確率 Pr[A+B] Pr[A+B]= Pr[A]+Pr[B]-Pr[AB] 加法定理
Pr[AB]=Pr[A]Pr[B|A]=Pr[B]Pr[A|B] 乗法定理
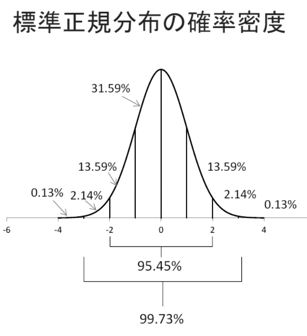
事象 A が起こっても起こらなくても事象 B の起こる確率に代わりが無いとき、事象Aは事象Bに対して独立である。 Pr[B|A]=Pr[B] (戻る) 正規分布 正規分布の式 正規分布は平均値µと分散σ2だけで記述され、その分布は 平均μを中心にして左右対称
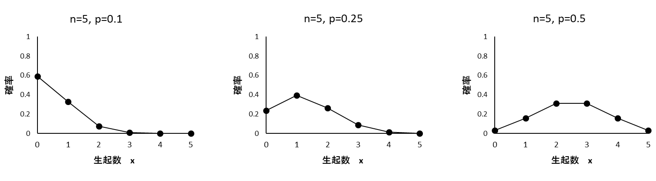
(戻る) 二項分布 出現確率pの事象が、n回中にx回現れる確率は n=5、pが0.1、0.25、0.5の二項分布
xは0からnの値を取り得るので、その確率をすべて加えると 二項分布の平均µと分散σ2は以下の式であらわされる。 μ=np σ2=np(1-p) (戻る) 略歴松田 りえ子(まつだ りえこ) 1977年 京都大学大学院薬学研究科修士課程終了 サナテックメールマガジンへのご意見・ご感想を〈e-magazine@mac.or.jp〉までお寄せください。 |
| Copyright (C) Food Analysis Technology Center SUNATEC. All Rights Reserved. |

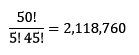
 が起こる確率 Pr[
が起こる確率 Pr[