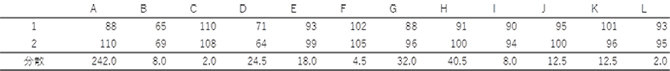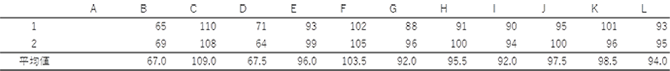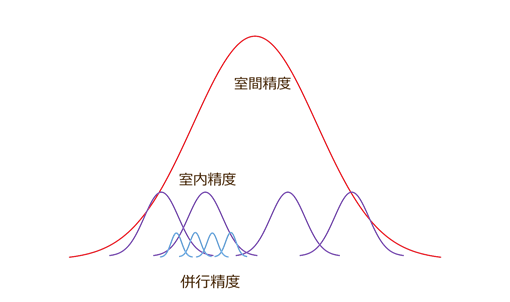
第1回から第3回では、基本的な統計について説明した。ここで示した、母平均あるいは母標準偏差の推定は、分析法の真度あるいは精度を推定する時に使用される。また、分析結果の品質の管理手法である、内部品質管理および技能試験の解釈は、第1回に示した正規分布の性質に基づいている。第4回は分析の性能評価と分析結果の品質管理の基礎となる統計について解説するとともに、これまでの回で解説した統計的考え方を復習する。

分析法の基本的な性能としては、選択性、真度、精度、定量限界、検出限界が挙げられる。この中で、真度と精度は実験データから統計的な考え方で推定される。

真度は、同一（とみなされる）試料をくり返し分析した結果の平均値と、その試料の濃度との差あるいは比で表される。一般に「回収率(recovery)」と言う用語が使われているが、回収率は試料からアナライトが抽出・精製されて測定系に到達する割合である。従って、液体試料をそのまま、あるいは希釈して測定するような分析系では、回収率と言う用語は原理的に使用できない。また、測定系にアナライトが入れば必ず正しい値が得られるという保証がない限り、測定系に到達する割合を推定することもできない。例えば、GCにおける吸着や、LC-MSにおけるイオン化阻害が起こると、100％の回収率があったとしても、真度は70%となるかもしれない。もちろん、逆の場合もあり得る。従って、分析系が正しい値を出せる性能としては、回収率ではなく真度を使用するべきである。

精度は、同一（とみなされる）試料をくり返し分析した結果の変動の程度である。くり返し分析を行うときの条件によって変動の程度が変わることは、容易に想像される。同じ試料を、一人の分析者が同時に分析した結果と、別々の分析者が行った結果では、変動の程度は後者が大きいと予想される。異なる試験所で分析を行えば、試験環境、分析者、分析器具・機器も異なるので、さらに変動は大きくなると予想される。このことから、精度ではくり返しを行った条件を示して
併行精度：一人の分析者が、同じ試料を同時に分析した結果の変動
室内精度：同一試験所内で、同じ試料を分析した結果の変動
室間精度：異なる試験所で、同じ試料を分析した結果の変動
のように区別する必要がある。
精度は標準偏差あるいは相対標準偏差として表され、通常は、併行精度≦室内精度≦室間精度である。Fig.1にこれらの関係を示す。図は分かりやすいように誇張して書かれているが、実際には、精度間にこれほどの差があるわけではない。

Fig.1 分析結果の分布と精度

　真度も精度も、同一（とみなされる）試料のくり返し分析結果の平均と標準偏差なので、同一試料を準備し、くり返し分析すれば求められる。このくり返し条件を一番広く設定したのが、試験室間共同試験である。試験室間共同試験では、異なる試験所が試料を分析するので、室間精度を推定することが可能である。室間精度が利用目的に妥当な程度に小さければ、通常の能力を持つ試験所ならば妥当な結果を出せると期待される。このため、Codex法やAOAC法のような、公定法と言われる分析法は、試験室間共同試験により室間精度が求められている。

試験室間共同試験の実施に当たっては、試験室数、試料数（マトリクス、濃度範囲）、解析方法を定めたプロトコルがISO 5725（Accuracy （trueness and precision） of measurement methods and results）および AOAC INTERNATIONALのOMA（Official methods of analysis）のAppendix D （Guidelines for Collaborative Study Procedures to Validate Characteristics of a Method of Analysis）として公表されている。ISO 5725は6つのパートに分かれており、JIS Z8402がこれらの一致規格となっている。以下、AOAC INTERNATIONALのプロトコルで使用されている統計手法を解説する。

試料の数は5、試験所数は外れ値を除いた後に8試験所が残ること、くり返し数は1が、最小限の必要事項とされている。試験所数として8が必要とされるのは、第3回で解説した通り、少ないデータから推定した標準偏差の信頼性は著しく低いためである。

試験室間共同試験では、精度推定に際して外れ値の検定が行なわれる。共同試験の目的は、その分析法の性能の推定であり、その前提は参加者から提供されたデータが一定の正規分布に従っていることである。明らかに正規分布に従っていないデータが存在すると、正しい真度あるいは精度が推定できなくなる。

外れ値の除外では、最初に、手順に正確に従っていないなどの、明らかに誤りであるデータを除外する。残ったデータに外れ値の検定を行う。この目的には、Cochran検定とGrubbs検定が使用される。全データに対して、Cochran検定、single Grubbs検定、pair Grubbs検定の順に検定し、棄却されなくなるまで繰り返す。また、棄却された試験所数が全体の2/9を超えてはならない。つまり、参加試験所数が10であれば棄却できる試験所数は2までである。試験所数が9の場合も2試験所を棄却できるが、そうすると試験所数が7になり試験所数の必要条件である8を満たさなくなる。

Cochran検定は併行分析した結果が他の試験所と比較して大きくバラついている試験所を除外するために行われる。試験所毎に併行分析した結果の分散を計算し、最も大きい分散／分散の総和をCochranの統計量とする。Cochran統計量の表（片側、2.5 ％）の試験所数とくり返し数に対応した値よりも、求めたCochran統計量が大きい時には、その試験所の値を棄却する。

Grubbs検定は併行分析した平均値が他と極度に離れている値がないかを検定する。最初にデータの平均値の標準偏差sを計算する。次に最も大きい平均値を除いた時の標準偏差s_Hと、最も小さい平均値を除いた時の標準偏差s_Lを計算する。これらの値から、平均値の最大値あるいは最小値を除いた時の減少率を以下のように計算する。


2つの大きい方をsingle Grubbs統計量とする。Grubbs統計量の表（両側、2.5％）の試験所数に対応した値と、求めた値を比較し、大きい場合には該当する試験所の値を棄却する。

single Grubbs検定で外れ値として棄却される試験所があった場合には、残ったデータに対してCochranの検定を行う。棄却される試験所が無ければ、pair Grubbs検定を行う。pair Grubbs検定では、平均値の大きい方から2試験所、小さい方から2試験所、平均の最大と最小の2試験所を除いた時の標準偏差を、 s_2H、s_2L、s_HLとする。これらの最大の値を用いて、single Grubbs検定と同じように標準偏差の減少を計算し、Grubbs表と比較して棄却を行う。

以下に計算の例を示す。
12か所の試験所（A-L）が2回くり返し分析を行ったデータと分散を示す。


分散の最大値はAの242.0である。分散の和は406.5なので、Cochran統計量は242.0/406.5×100=59.5である。このCochran統計量は、Cochranの表の試験所数12の値である59.2より大きいので、試験所Aの値を棄却する。

くり返し数が2回の時のCochranの表

残った11試験所の2回くり返しデータの平均を求める。



平均の最大は109.0（C）、最小は67.0（B）である。平均値全ての標準偏差は13.233、最大を除いた標準偏差s_Hは12.627、最小を除いた標準偏差s_Lは10.859であり、減少率はそれぞれ4.58と17.94となる。試験所数11のGrubbs表のone highest or lowestの値である39.3より小さいので、これらの試験所は棄却されない。最初の試験所数は12であり、その2/9は2.67なので、棄却できる最大数は2である。従って、pair Grubbsによってさらに2試験所を除くことはできないので、検定はこれで終了する。

参考のためにpair Grubbs検定を行う。平均の大きい方から2つは、109.0（C）と103.5（F）、小さい方から2つは67.0 （B）と67.5 （D）であり、s_2H=12.464、s_2L=5.570、s_HL=10.181それぞれの減少率は5.81、57.91、23.07となる。試験所数11のtwo highest or lowestの値は52.5であり、減少率57.9はこれより大きいので、BとDの試験所が棄却の対象になる。

 

Grubbsの表

 

外れ値を除去した残りのデータから、分析法の真度と室間精度を求める。くり返し分析がされていれば、併行精度が求められる。試料の分析が併行条件ではなければ、室内精度になる。

真度（バイアス）は、全データの平均値と試料に付与された値の差として求められる。くり返し分析が行われていなければ、データの標準偏差が室間精度となる。くり返しがある場合には、データに一元配置の分散分析を行って室間標準偏差と併行標準偏差を推定する。

室間共同試験での分析値は以下のようなモデルで表される。
分析結果　＝　平均値　+　σ_L（室間変動）  + σ_r （ランダム変動）
併行分析の変動はランダムに発生し、その変動の大きさはどの試験所でも同じと仮定する。くり返し数をn、試験室の数をlとすると、データ総数はnl個となる。データ全体の標準偏差にはσ_L（室間変動）とσ_r（ランダムあるいは室内変動）が含まれるので、そのまま室間精度とすることはできない。このように2種類の変動が重なっている時に、個々の変動（分散）を推定するために、一元配置分散分析が行われる。
一元配置分散分析のデータの構造は以下のようである。
d11     d12・・・・d1n
d21    d22・・・・d2n
・
　・
　dl1     dl2・・・・dln
同じ行のデータは同一の試験室から得られているので、室間変動は含まれていない。つまり、分析結果に含まれるσ_Lは行内では一定なので、変動に寄与せず、行のデータの平方和S1-Slには併行分析の変動だけが含まれる。（平方和については第3回を参照）

　d11     d12・・・・d1n               S1
　d21    d22・・・・d2n               S2
　・
　・
　dl1     dl2・・・・dln                 Sl

 

S1-Slの総和をS_rとすると、S_rにはn回のくり返しのlセットのデータが含まれており、自由度は(n-1)×lである。平方和を自由度で割れば分散V_rが得られる。

 

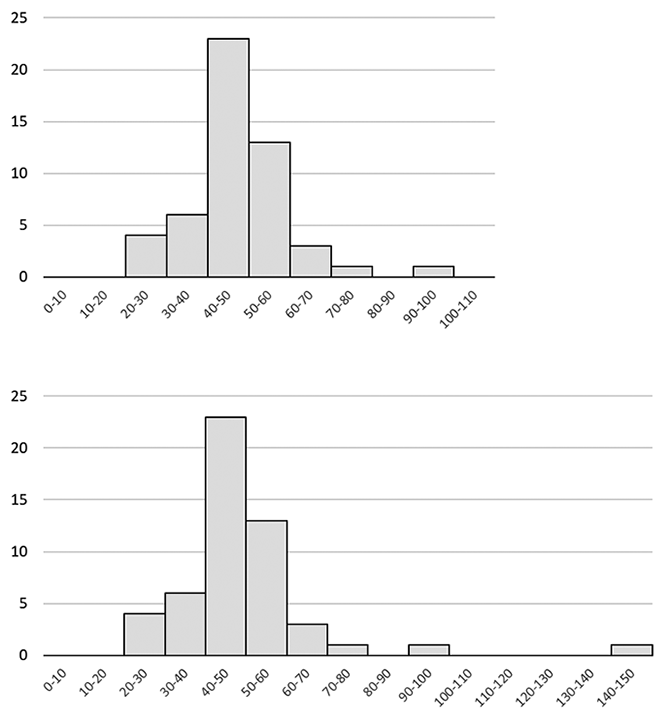
総平方和S_tの自由度はln-1、S_rの自由度は(n-1)×lであり、総平方和S_tからS_rを差し引いた残りの平方和S_t-S_rの自由度は、ln-1-(n-1)×l=ln-1-ln+l=l-1となる。
　 総平方和 S_tからS_rを差し引いた残りの平方和には、各行でのランダムな変動の寄与を除いた変動が含まれる。行の平均値の変動はσ_Lとσ_r/nの和であり、各行にn個の平均値があるので、S_t-S_rをその自由度l-1で割って得られる分散は、σ_L（室間の変動）の2乗(V_L)×nとの和である。V_rは求められているので、

となる。分散V_LとV_rの平方根が室間の変動の標準偏差σ_Lと、くり返しの変動の標準偏差σ_rとなる。試験室が1回分析した結果の分散は、V_rとV_Lの和となるので、が室間精度となる。

Excelには一元配置の分散分析が組み込まれている。実行すると、下のような分散分析表が表示される。

グループ内の分散がV_rに当たるので、これの平方根が併行精度σ_rとなる。グループ間の分散はV_L×nV_rである。これから、上記の計算で室間精度を求めることができる。

分散分析の本来の目的は、グループ内の変動とグループ間の変動に差があるかの検定である。この目的でF検定が用いられ、分散比とF境界値を比較する。

農薬等あるいは有害物質の分析法の妥当性評価ガイドラインは、単一の試験所が分析法の妥当性を確認する方法を示している。ここで、真度と室内精度を同時に推定する方法の例として枝分かれ実験が示されている。この結果の解析も、一元配置の分散分析により行うことができる。試験室間共同試験では室間の分散V_Lが推定されるが、室内の枝分かれ実験では室内の分散が求められる。

技能試験は、室間共同試験とよく似た形式で実施されるためか、時として混同されることがある。しかし、室間共同試験と技能試験は目的が全く違っている。前者の目的は分析法の性能を推定することであり、後者は分析を行う試験所の能力の評価が目的である。従って、技能試験では指定された分析法のプロトコルに従う必要はなく、実際にその試験所が実施している方法で分析結果を得て、それを報告する。

参加試験所の結果を用いてz-スコアを計算し、これによって試験所の能力を評価する。参加試験所の結果が平均μ、標準偏差σの正規分布に従っているとする。この時試験所iの報告値x_iのz-スコアを次のように計算する。

規分布の性質（第1回参照）から、| z -スコア| ≦ 2 となる確率は95.45 %、2 < | z-スコア | < 3となる確率は4.28 %、| z-スコア | ≧ 3となる確率は0.26％であるので、これに基づいて
| z -スコア | ≦ 2 ：満足
2 < | z -スコア | < 3　：疑わしい
|　 z -スコア | ≧ 3 ：不満足
と評価される。
このような評価が可能となるためには、参加試験所の結果が平均μ標準偏差σの正規分布に従っていなければならない。しかし、報告値には他の値とかけ離れた、分布から外れた値が含まれることが、しばしばある。報告値から平均μと標準偏差σを計算すると、外れ値が平均μと標準偏差σに影響を与え、その結果として評価が不適切になることがある。

Fig.2に仮想的な技能試験結果を示す。上の例では50試験所がまとまった分布を示し、1試験所がやや外れている。平均値は48.24、標準偏差は12.19であり、やや外れていると思われる試験所のz-スコアは4.0と計算された。しかし、もう一つの外れ値が加わった下のような場合には、平均値は50.10、標準偏差は18.05となり、先ほどz-スコアが4.0であった試験所のz-スコアは2.6となった。このように、大きく外れた値が含まれると、特に標準偏差が大きくなる。その結果、本来は| z -スコア | ≧ 3で不満足と判定されるべき試験所の評価が変わってしまう。

このような外れ値への対応として、室間共同試験ではCochran検定およびGrubbsの検定が行なわれるが、技能試験ではロバスト統計量を計算する。ロバスト統計手法は外れ値を除去することなく、外れ値以外の値の平均値と標準偏差を推定する方法である。平均値に対応するロバスト統計量としては中央値、標準偏差に対応するロバスト統計量としては中央絶対偏差(MADe)がある。中央値は、データを大きさの順に並べたときの中央となる値であり、 n個の数値を昇順に並べたものをx_iで表すと、nが奇数の時の中央値は



Fig.2　外れ値を含む技能試験結果

nが偶数の時の中央値は

となる。x_iと中央値の差の絶対値の中央値を求め、それに1.483を乗じるとMADeが得られる。いずれも、データの中の順位に基づいており、端にある値の大小には影響されない点で、ロバスト（頑健）な統計量となっている。

また、中央値と中央絶対偏差を初期値とし、くり返し計算によってロバスト平均値とロバスト標準偏差を求める、アルゴリズムAという手法もよく用いられる。

内部品質管理は、分析システムが統計的管理状態にあることの継続的確認のために行われる。統計的管理状態にあるシステムでは、一定の濃度の試料の分析結果は、一定の分布を示す。通常は正規分布に従うことを前提として、上記の技能試験の場合と同じように、z-スコアによる評価が行われる。内部品質管理におけるz-スコアの計算に用いる、平均μと標準偏差σはそれぞれの試験所での測定結果から決定する。

この平均μと標準偏差σが維持されていれば、| z-スコア | ≧ 3となる確率は0.26％である。この確率は非常に小さいので、たまたまその事象が現れたと考えるよりは、平均μと標準偏差σが変化したと考えることが合理的である。これは統計的管理状態ではなくなったということで、バリデーション結果による分析結果の品質保証ができなくなる。従って、何らかの対処により統計的管理状態を再度確立することが必要である。2 < | z-スコア | < 3となる確率は4.28 %であり、20回から25回に1回はこのようなスコアになる。この時は、確率に従ってその状態が出現したのか、平均μと標準偏差σが変化したのかは判断できないので、その後の状態に注意する必要がある。

内部品質管理は継続して実施することが基本であり、一回一回のz-スコアで判断するだけではなく、経時的な変動を考えるべきである。例えば、2 < z-スコア< 3となる確率は2.14 %であるが、これが2回連続して出現する確率は2.14 %×2.14%=0.046％である。この確率は| z-スコア | ≧ 3となる確率より低く、平均μと標準偏差σが変化したと考えるべきであろう。同様に出現確率の低い状況としては、z-スコア≧ 1あるいはz-スコア≦ -1が4回連続する確率は非常に小さい。また正あるいは負のz-スコアが10回連続する確率は(0.5)¹⁰=0.1%で、これも| z-スコア | ≧ 3となる確率よりも小さい。個々のz-スコアから「満足」という評価が得られたとしても、上記のような現象が見られた場合は、統計的な管理状態が維持されていない可能性が高いので、原因究明を行うべきである。

以上のような議論が成立するためには、内部品質管理に使用している平均μと標準偏差σが正しいことが大前提である。内部品質管理を実施する前に、それぞれの分析系の平均μと標準偏差σを正しく推定することが重要である。このためには、十分なくり返し数を用いるとともに、試験所内での重要な変動をすべて含むような実験計画に基づいて推定するべきである。