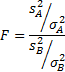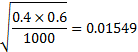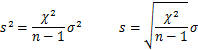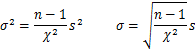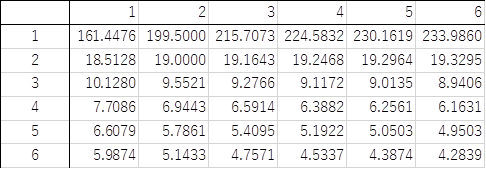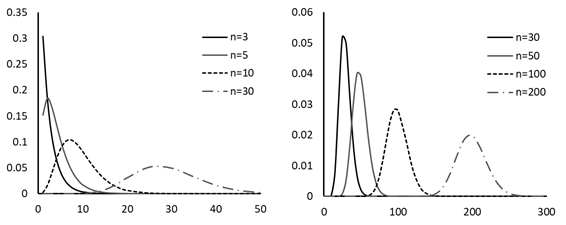
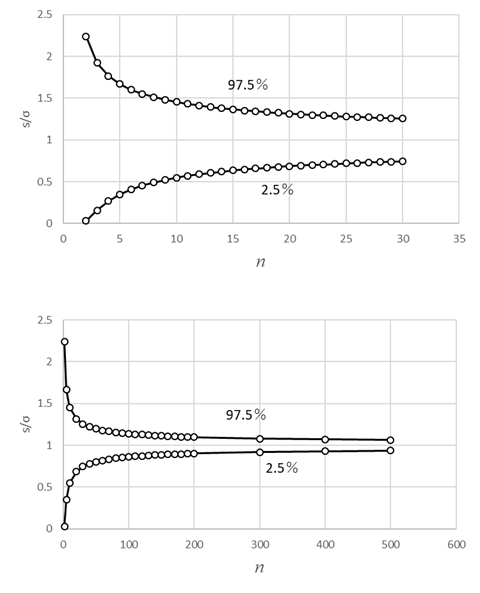
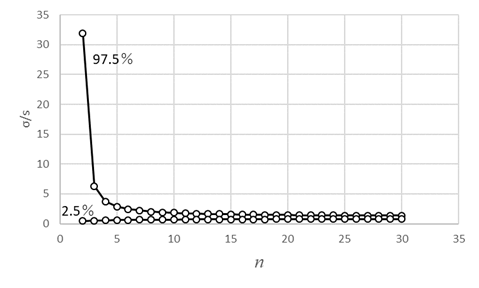
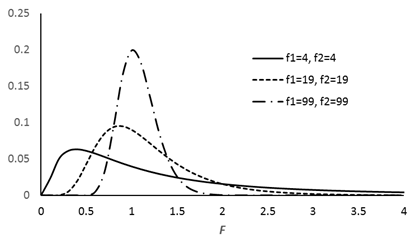
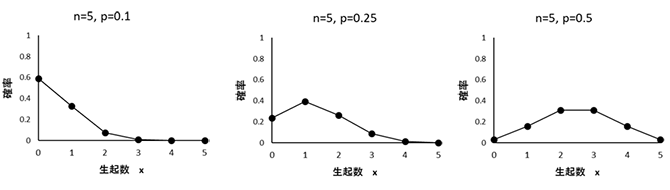
第2回では、標本から母平均を推定する、あるいは検定する方法を説明した。
・大標本から標本平均 、標本分散 s²が得られたとき、母平均 μ の95%信頼区間は

となる。 ・小標本から標本平均 、標本分散 s²が得られたとき、母平均 μ の95%信頼区間は

となる。 ・以上の関係に基づいて、母平均の差の有意性を検定できる。

第3回は、母分散及び母割合を推定・検定する方法を解説する。

母集団が正規分布しているとすれば、無作為に抽出した標本の平均（標本平均）の期待値は母平均 μ に等しい。同様に、無作為に抽出した標本の分散（標本分散）s²の期待値は母分散σ²に等しい。しかし、標本平均と異なり、標本分散の分布は正規分布ではない。
　 分散の分布の解説の前に、平方和（偏差平方和）S を考える。標本の平方和Sは

で表される。nは標本の大きさであり、標本分散s²=S/(n-1)である。このとき平方和と母分散の比をχ²とすると

は自由度f=n-1の χ²分布をする。χ²分布の期待値は f＝n-1 である。しかし、標本分散の平方根である標本標準偏差sの期待値は、母標準偏差σとは一致しない。sの期待値とσの比は、n=3では0.8862、n=5では0.9400、n=10では0.9727であり、小標本で得られる標本標準偏差の期待値は母標準偏差よりも小さくなる。つまり、小標本から求めた標本標準偏差は、母標準偏差の不偏推定値ではない。
　 母分散の推定は、平均値の推定の場合のt分布の値の代わりにχ2分布の値を使って行われる。
 なので、の95％範囲は

となる。逆数として、さらにSを掛けると

となり、母分散の信頼区間が得られる。第2回と同じ例を示す。
例　採取した5試料中の物質Aの濃度を測定したところ、5個の測定結果の平均値（標本平均）が0.0254 mg/kg、標準偏差（標本標準偏差）が0.0067 mg/kgであった。
標本分散は標本標準偏差の2乗なので、0.0067×0.0067=0.00004489
平方和 Sは標本分散（s²）×(n-1)なのでS=0.00004489×(5-1)=0.00017956
自由度4のχ²分布の値は、2.5％では0.4844、97.5％では11.14であるので

1.611E-05≤σ²≤0.0003707
平方根を計算すれば
0.004015≤σ≤0.01925
となる。95％区間の上限は得られた標本標準偏差の3倍近い値である。
同様の値が100個の測定結果から得られたならば、平方和は
0.0067×0.0067×99=0.004444
自由度99のχ²分布の値は、2.5％では73.36、97.5％では128.4なので、

0.005883≤σ≤0.007783
となり、母標準偏差の95％区間の幅は小さくなる。また、3回の測定結果から推定すると、χ²分布の値は、2.5％では0.0506、97.5％では7.3778と小さいので、母標準偏差の範囲は　0.003488≤σ≤0.04211　となり、非常に広くなる。つまり、少数の試行から計算した標本標準偏差の値は信頼性が極めて低い。

平均値ではt検定により、母平均の差の検定が行われたが、分散の場合は比の検定が行われる。分散の比の検定には、下式で表される統計量Fが使われる。

Fの分母、分子共に、標本分散と母分散の比になっている。標本分散の期待値は母分散に等しいので、Fの期待値は1となる。また、標本分散と母分散の比はであり、χ²分布は自由度（n-1）により異なるので、Fの分布も分子と分母の自由度によって変化する。
　ある物質の分析を、方法Aと方法Bで行い、以下のような結果が得られたとする。
方法A　0.5128　0.5258　0.4987　0.4825　0.5285
方法B　0.5421　0.5341　0.4845　0.4972　0.4852　0.5574　0.5026
平均値は方法Aが0.5097、方法Bが0.5147であり、平均の差の検定では有意差は見られない。一方、標準偏差を見ると、方法Aは0.0193、方法Bは0.0294であり、方法Bのばらつきの方が大きいかもしれない。このような時に、分散の比の検定（F検定）を行う。
分散の比の検定では、t検定の場合と同様に、「2つの母分散は等しい」を帰無仮説とする。そうすると、となるので、となり、標本分散の比を求めて、F表の値と比較すれば検定が行える。
　F表は上側確率のみ示されている（1より大きい値のみ示されている）ので、Fを計算する場合には、分散の大きい方を分子にする。方法Aの分散は0.0003708、方法Bの分散は0.0008462であるので、方法Bの分散を分子としてFを計算する。

この値を、F表の対応する自由度の値と比較する。この場合は分子になった方の自由度が6、分母の自由度が4である。危険率5％のF表で自由度が6と4の値は6.1631であるので、得られたFの値はこれより小さく、帰無仮説は否定されない。つまり、方法Aと方法Bの分散（あるいは標準偏差）は異なるとは言えないという結論になる。
　上の例では分散の比が6.1631、つまり標準偏差の比がおよそ2.5以上にならないと帰無仮説が否定されない。2つの方法の繰り返し数が3であれば、標準偏差の比が4.36以上にならないと帰無仮説は否定されない。つまり、わずかに精度が優れていることを示すためには、かなり多い試行数が必要となる。
　 第2回で解説した対応のないt検定では、帰無仮説として母平均は等しいとしている。この時に母分散も等しいと仮定している。従って、標準偏差が極端に違っているとこの仮定が成立しないため前提が満たされず、t検定もできなくなるので、まずF検定により分散が等しいという帰無仮説が否定されないことを確認する必要がある。

前項までは特性が計量(variable)である母集団からの標本から、母数を推定あるいは検定する手順を解説した。母集団の特性値が属性(attribute)である場合には、ある属性の母集団の中の割合を推定あるいは検定する。
　 報道では、「調査により○○は21％でした」のような表現がよく見られる。自ら調査して割合を報告することも多い。このような場合に報告される値は標本割合である。標本の大きさをn、対象となる特性が現れた数をχとすると、標本割合は
　 である。
　 第1回で説明したように、標本割合の分布は二項分布に従う。二項分布は、標本の大きさnと特性の確率pで記述される。出現確率pの事象が、n回中にχ回現れる確率はで表される。χが取り得る値は0からnであり、

である。
　標本割合の期待値はpに等しく、の分散は

である。nが大きい場合には、二項分布は正規分布で近似でき、一般にnpが3以上であれば、正規分布で近似できるとされている。p = 0.1であれば30以上のnが必要であり、p=0.5であればnは6以上あればよい。

例
　50人にアンケート調査を行ったとき、質問Aに「そう思う」と答えた人が20人いた。この時の質問Aに賛成する人の割合の信頼区間を推定する。
　標本割合 は20/50=0.4である。pの推定値としてを用いれば、np=20>3であり、正規分布で近似することができる。の分散は

であり、標準偏差は0.06928となる。正規分布近似で母割合pを推定すると
0.40-1.96×0.06928<p<0.40+1.96×0.06928
0.2642<p<0.5358
となり、質問Aに賛成する人の割合は26％と54％の間という推定が得られる。
　 分散の計算の分母はnなので、同じであっても、標本の大きさにより分散は変化する。が同様に0.4であったとしても、1000人の調査であった場合には、標準偏差は

になり、母割合pの区間は37%～43%である。大きさ50の標本の場合と比較して割合の信頼性は大きくなる。調査結果を見る時には、割合だけではなく標本の大きさを考えることが重要である。

平均、分散と同じく、割合においても標本の大きさは母数の推定区間に大きな影響を与える。標本の大きさが50の時の割合の区間が大きいことから、少数の標本から得られた割合の大小の比較は困難であることが容易に予想される。

例
　女性30人、男性20人にアンケート調査を行ったとき、質問Aに「そう思う」と答えた人が女性は15人、男性は12人であった。この時の質問Aに賛成する人の割合は男女で差があるか？
女性の割合　　　男性の割合　
全体の割合　

帰無仮説は「男女に割合の差はない」つまり、である。
正規分布を仮定すると、が予想される差の標準偏差の1.96を超えた場合には、帰無仮説が否定される。の分散はであるので、誤差法則 により差の分散は

となる。数値を代入すると

となり標準偏差は0.1439と計算される。この1.96倍は0.2820である。
の絶対値0.1は、0.2820より小さいので帰無仮説は否定されず、男女に賛成割合の差があるとは言えないことになる。この場合の分散の計算にも標本の大きさが含まれている。上記の例で割合は同じで女性が300人、男性が200人の調査であれば、分散が0.00207、標準偏差が0.0455、標準偏差の1.96倍は0.08918となる。そうすると、帰無仮説が否定され、男女に差があるという結論が導かれる。
動物実験あるいは微生物分析で2つの処理による割合（死亡率、検出割合など）を比較することがある。2つの標本の大きさが10程度の時に、割合が0.3と0.6で割合の差が0.3であったとしても、
分散：
標準偏差＝0.2225
標準偏差×1.96＝0.4361
となり、帰無仮説を否定することができない。実験計画を立てる時には、予想される割合の差と、検定に必要な標本の大きさを考慮すべきである。

偏差平方和Sをσ2で割った値がχ²である。


標本分散s²=S/(n-1)なので

正規分布N(µ,σ2)から大きさnの標本を抽出すると、χ²は自由度f (=n-1)のχ²分布をする。χ²分布の期待値は　f=n-1 であり、分散は2fである。下にnが3～200の時のχ²分布の確率密度を示す。

図の横軸はχ²分布の値、縦軸は確率である。n=10の場合に、標本分散s²が母分散σ²に等しければ、χ²の値はn-1=9となる。n=10のχ²の値をみるとχ²が7の時が最も大きくなる。つまり、n=10の標本では、母分散よりもやや小さい標本分散が得られる確率が最も高い。n=3の場合では、χ²=1つまり、母分散の1/2の大きさの標本分散が得られる確率が30％程度である。標本の大きさnが小さいときのχ²分布は、非常に対称性が悪いが、nが大きくなると次第に対称になり、正規分布に近づいてくる。

を変形すると

となる。χ²が0.025と0.975となる値を求めれば、s/σの95%区間が得られる。

標本の大きさnが大きくなるとともに、s/σの95%区間は小さくなる。つまり推定の信頼性が向上する。nが10より小さい範囲では、s/σの区間は広く、nが3の時には0.16-1.9である。3回の繰り返しで標準偏差を求めると、真の標準偏差の1/5から2倍程度の値が得られることになり、正しく推定できるとは言い難い。
　 標本標準偏差から母標準偏差を推定する場合の95％区間は

となる。下の図はσ/s の95％区間のプロットである。

少数のデータからの母標準偏差推定の区間が非常に広く、また対称ではなく大きい側に広がっていることがわかる。

（戻る）

図に自由度1(f₁)と自由度2(f₂)が4、19、99のとき、つまり2つの標本の大きさが5、20、100の時のF分布を示す。自由度が大きくなるにつれてF分布は対称になり、正規分布に近づく。

F分布表には、上に自由度1、左側に自由度2が示されており、交わるところに2つの自由度において右側の確率が5%（2.5%、1%）になるFの値が示される。

（戻る）

二項分布は、標本の大きさnと特性の出現確率pで記述される。
出現確率pの事象が、n回中にχ回現れる確率は

で表される。二項分布の形は大きさnと特性の出現確率pで変化する。
下の図はn=5で確率pを変えたときの二項分布を示す。
n=5、pが0.1、0.25、0.5の二項分布

χは0からnの値を取り得るので、その確率をすべて加えると

である。二項分布の平均μと分散σ2は以下の式で表される。
μ=np
σ²=np(1-p)

（戻る）

2つの独立な確率変数χ₁（平均=μ₁、分散σ₁²）とχ₂（平均=μ₂、分散σ₂²）の
和 y=χ₁+χ₂と差z=χ₁-χ₂の期待値と分散は


となる。

（戻る）