
不確かさ評価入門
 国立研究開発法人 産業技術総合研究所 計量標準総合センター
物質計測標準研究部門 計量標準基盤研究グループ
主任研究員 田中 秀幸
1.はじめに
近年、試験所認定制度の広まりとともに不確かさ評価についての重要性が高まってきている。本解説では、試験所認定制度と不確かさとの関係、不確かさとは何か、ごく初歩的な不確かさ評価法について解説する。
2.試験所認定制度と不確かさ
近年、試験・校正結果の信頼性を担保するため、試験所認定制度を導入する機関が増え始めている。試験所認定制度とは、その試験所が信頼できる試験・校正結果を出すための技術的能力を十分に持っており、また試験所を公平・公正に運営していることを認定機関と呼ばれる第三者によって審査・認定を行う制度のことである。この試験所認定は、「ISO/IEC 17025(JIS Q17025)試験所及び校正機関の能力に関する一般要求事項1)」に基づいて審査される。
先ほど触れたようにこの試験所認定では技術的能力だけではなく、試験所の運営についても審査される。それには要員の管理や文書管理、クレーム処理などについての事項が存在し、トップマネジメントから下請負契約まで試験所の運営に関する事柄について詳細にチェックが行われる。
技術的能力の審査は、要員・設備・装置の能力に関して行われるが、それは測定・試験・校正結果の精確さの担保が目的である。そのためにISO/IEC 17025において重要視されているのが測定のトレーサビリティの確保である。用いる測定器から正しい測定結果を得るためにはその測定器が正しく校正されている必要がある。校正とは、用いている測定器よりも精確さが高い測定器・実量器・標準物質(これらは「標準」と呼ばれる)を用意し、その値と校正したい測定器の示す値を比較し、どのくらいかたよりが存在しているのかを決定するという作業を意味する。つまり、より良い値と測定器の値を比較するので、測定器がどのくらいのかたよりを持っているかを知ることができるわけである。
しかし、この校正だけでは精確さの担保はできない。なぜなら用いた精確さの高い測定器・実量器・標準物質自身がどの程度値が正しいのかが分からないからである。つまり、精確さの高い測定器・実量器・標準物質もさらに精確さが高い測定器・実量器・標準物質によって校正される必要がある。そう考えると、この校正をどんどん繋げていき、最も精確さが高いと考えられるものまで結びつかなくては完全に精確さの担保ができたとはいえないであろう。
もし、用いている測定器に対して、この校正の連なりが最も高いレベルまで繋がったということが分かったとしよう。この場合に「測定のトレーサビリティが確保できた」ということができるのである。つまり、トレーサビリティとは、校正を連ねていき、最も精確さが高いと考えらえるものまで結びついている、という性質のことを表している。
次にここで触れられている、最も精確さが高いと考えられるもの、とは何を指しているかを考えよう。世の中では様々な測定が行われているが、その測定結果は通常SI単位を用いて表される。昔、国や地方によってばらばらな単位が用いられていた(日本では尺・貫、イギリスではヤード・ポンドなど)が、商取引のボーダレス化に伴い、現在では世界的な合意によって同じ単位を用いることが取り決められている。そこで用いられているのがSI単位である。SIは7つのSI基本単位とそれを組み合わせたSI組立単位からなる単位系であり、それぞれの単位の大きさが量の定義として定められている。例えば、1 mの大きさは、1秒の299 792 458分の1の時間に光が真空中を伝わる工程の長さ、と定義されている。これがすべての単位について定義されており、この世の中で広く使われている。
しかし、誰かがこの定義を実現し、それを供給しなければならない。そこで世界各国は「国家標準研究所」と呼ばれる研究所を自国内で設立し、そこでSI単位の定義を基にした最も精確さが高いと考えられるものを作り出し、民間に供給しているのである。日本の国家標準研究所は主に産業技術総合研究所 計量標準総合センターが担当し、民間に対して標準供給と呼ばれる、最も精確さが高いと考えられる値の供給業務を担っている。また、自国だけでSI単位の定義に従った値を作り出したとしても、本当にそれが問題なくSI単位の定義を実現しているかどうかはわからない。よって各国の国家標準研究所が集まり、値を比較しあうことにより、本当にSI単位の定義が実現できているかどうかを確認する国際比較と呼ばれるいわば技能試験も行っている。
このようにして校正の連鎖が最も精確さが高いと考えられるものまで到達するシステムを構築しているわけであるが、これだけでは精確さを担保するには不十分なところがある。先ほど触れたように、校正により用いている測定器がどの程度かたよりがあるのかを知る、ということを行っていたとしても、これだけではばらつきに関しては何も触れられていない。つまり、上位標準が示す値と用いている測定器の示す値の差が分かっていたとしても、その作業を行う、例えば質量でいえば、分銅を精密天秤に乗せ、分銅と天秤の示す値との差がどれくらいあるか、ということを調べたとしても、この手続きを繰返して行うと、分銅と天秤の示す値が一定の値にはならず、ばらつきを持つはずである。このばらつきの評価なしに精確さを担保することはできない。
ここで、トレーサビリティの定義2)を見てみよう。
トレーサビリティ・・・個々の校正が測定不確かさに寄与する、文書化された切れ目のない校正の連鎖を通して、測定結果を計量参照に関連付けることができる測定結果の性質。
この定義を簡単に見てみると、校正を連鎖させ、計量参照まで関連付ける、とある。「計量参照」という言葉は非常に分かりにくいが、とりあえず、国家標準研究所によるSI単位の定義を実現したもの、と考えればよい。そうすると、校正を連鎖させ、SI単位の定義まで繋がっている、ということになる。これは今まで解説した内容に相当していることがわかるだろう。あとは最初の部分、「個々の校正が測定不確かさに寄与する」という部分である。これは、トレーサビリティ構築のため各階層で行われている校正において「不確かさ」がすべて表明されていなければならないことを意味している。つまり、校正によってかたよりがわかるが、さらにその校正の時点で表れるばらつきを不確かさとして評価しなければならない、ということである。このように校正によってかたよりを、その校正の作業時に表れるばらつきを不確かさとして表すことによって精確さを担保するということである1。トレーサビリティの確保は、この校正の連鎖と校正時の不確かさの表明がセットで行わなければならないということである。
まとめると、試験・校正結果の客観的な信頼性をユーザーに提示するために試験所認定制度が用いられており、その試験所認定制度の認定を受けるためには測定におけるトレーサビリティを確保する必要があり、トレーサビリティを確保するためには不確かさ評価が必須となる、ということである。
1 現在の「校正」の定義2)では、標準の値と測定器の指示値との関係を示すだけではなく、不確かさも表明しなければならないと定められている。
3.不確かさとは何か
不確かさとは、先ほどトレーサビリティの解説にて紹介したように、測定結果のばらつきを示すものである。不確かさの定義3)を次に示す。
不確かさ・・・測定の結果に付随した、合理的に測定対象量に結び付けられ得る値のばらつきを特徴付けるパラメータ。
つまり、「値のばらつきを特徴付けるバラメータ」とあるように、測定結果のばらつきを表すものである。しかし、不確かさにおいて、「ばらつき」という言葉には注意が必要である。「ばらつき」といって普通イメージするのは、繰返し測定などを行ったとき、測定結果が全く同じ値にならず、若干違う値が得られた、というものだろう。もちろん不確かさ評価においてはこれもばらつきであるが、以下のようなものもばらつきとして考える。
例えば、測定を行っている部屋にデジタル温度計が置いてあり、その温度計を見たところ、20 ℃と表示されていたとしよう。普通に考えると、この測定結果は20 ℃であり、そこにはばらつきは存在しないが、もう少し考えると、20 ℃という表示だったからといって、室温が20.000000… ℃であるということを意味しているわけではない。あくまでも最小表示桁が1 ℃であったため、20 ℃と表示されていたにすぎず、実際の室温は、19.5 ℃から20.5 ℃の間に存在している、ということを表しているだけである。つまり、本当の室温は19.5 ℃から20.5 ℃の間のどこに存在しているか分からないわけである。結局どこにあるか分からない、というのはばらつきと意味合いでは同様であろう。このような知識の不完全さ、というものに関しても不確かさではばらつきとして扱う。
次に「測定の結果に付随した」というところに注目しよう。測定の結果に付随した、ということは、不確かさとは、測定の結果、つまり何か測定された結果などの「値」に付くものである。これは、不確かさは測定器や測定システムには付かない、ということを意味する。あくまでも、何らかの測定器で測定を行い、その測定された値に不確かさが存在する、ということを表しており、例えば、今回測定に用いた精密天秤の不確かさ、というものは存在しない。不確かさは測定装置には付かない、ということである。あくまでも測定された値に不確かさは付くということである。
しかし、一般的に「精密天秤の不確かさ」をはじめとした「測定器の不確かさ」という用語はよく使われている。これらは「測定器の校正の不確かさ」のことを略して「測定器の不確かさ」と言っている場合がほとんどである。
では「測定器の校正の不確かさ」とは何だろうか?測定器は上位標準によって校正される。例えば、精密天秤では、標準分銅を用いて校正を行う。この作業は、標準分銅の値と精密天秤の値を比較し、精密天秤の目盛に値付けをする、ということを行うが、その値付けされた目盛は完全に正しいわけではなく、その目盛は不確かさを持つはずである。この目盛が持つ不確かさのことを「精密天秤の校正の不確かさ」と呼ぶわけである。
つまり、トレーサビリティのところで解説した、校正時の不確かさ、というのがこの「測定器の校正の不確かさ」であり、トレーサビリティ確保のためには校正が行われるところすべてにおいて、この校正の不確かさを評価し、明示する必要がある。そうすると、自前ですべての校正の不確かさを求める必要があるように思うが、そこまでは行わなくてもよい。なぜなら試験所認定を受けた校正機関による校正がなされた測定器には校正証明書が添付され、その校正証明書にはトレーサビリティが確保されている、という内容と、さらにその校正機関が評価した校正における不確かさが記載されている。よってこの校正証明書があれば、その測定器の校正まではトレーサビリティが確保されている、という証明となる。
では次に、トレーサビリティが確保された測定器を用いて、実際に測定を行ったときのことを考える。次にあげる例は、トレーサビリティが確保されている精密天秤を用いて試薬の質量を測定したものである。その場合のトレーサビリティと不確かさに関する模式図を図1に示す。
実験室で使用している精密天秤は、試験所認定を受けた校正機関で校正されているとしよう。その場合、校正機関はトレーサビリティが確保された標準分銅を用いて精密天秤を校正している。標準分銅にはさらに上位の校正機関によって校正された結果が記載された校正証明書が添付されており、その校正証明書には標準分銅の校正の不確かさが記載されている。その標準分銅を用いて精密天秤を校正すると、標準分銅の校正の不確かさがそのままばらつきとして精密天秤の校正値に影響を与えるはずである。よって標準分銅の校正の不確かさは、精密天秤の校正の不確かさの一要素となるはずである。さらに、校正作業を行うと、その作業で引き起こされるその他要因のばらつき、(繰返しのばらつきや、温度・湿度・気圧のばらつき)が存在し、それらが合成されて、精密天秤の校正の不確かさとなり、その不確かさが精密天秤の校正証明書に記載されている。
次に精密天秤を用いて試薬の質量を測定した場合、その測定された試薬の質量の不確かさを求めることを考えると、先ほどの分銅の場合と同じく、精密天秤の校正の不確かさは、試薬の質量の不確かさの一要因となり、さらに作業に伴うその他要因の不確かさと合成され、試薬の質量の不確かさを求めることができるのである。
よって、ここで混同してはいけないのが、天秤の校正の不確かさと試薬の質量の不確かさである。天秤の校正の不確かさはあくまでも、天秤の目盛がどの程度正しいのかを表しているにすぎず、その天秤を用いて測定された試薬の質量の不確かさを表しているわけでない、ということである。精密天秤を用いて測定される試薬には、例えば吸湿性が非常に高いものや、揮発性が高い物質も存在するわけであり、そのような場合には、試薬の性質によって、試薬の質量の不確かさが変わってくるのは当然である。よって、測定器の校正の不確かさと、測定器を用いて測定した結果の不確かさを混同してはならず、厳密に区別して考える必要がある。
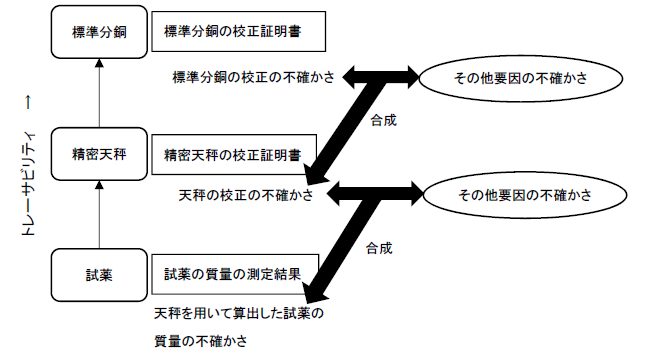
図1:測定・校正の不確かさとトレーサビリティ
4.不確かさの算出法
これまで見てきたように、不確かさとは測定結果のばらつきを表すものである。ここでは簡単に測定結果のばらつきの大きさをどのように求めるのか、ということについて原理を紹介する。
不確かさを評価するためにまず必要なのが、ばらつきを与える要因、つまり「不確かさ要因」を決定することである。不確かさ要因は大きく分けると、測定装置が原因、測定という行為そのものが原因、測定されるものが原因、測定環境が原因のものがある。細かく見るためには、その行っている測定についての知識が非常に重要になり、また、不確かさ要因は測定の種類によって非常に多岐にわたるので、ここでは深くは触れない。ただ重要なのは、最終結果に大きな影響を与える要因だけを考慮する、ということである。ほとんど効かない要因に対して厳密な不確かさ評価を行ったとしても最終結果は全く変わらず、無駄骨であったということもよく起こる。
次に各不確かさ要因から引き起こされるばらつきの大きさを求める。不確かさ評価ではばらつきの大きさを標準偏差で表す。標準偏差とはいわば「ばらつきの平均値」である。つまり、繰返し測定を行い、ばらつきのあるデータを得たとすると、そのデータの中には、平均値から大きく離れたデータ、あまり離れていないデータと様々なものが含まれるはずである。このとき、測定データが平均的にどの程度平均値から離れているか、ということを計算したものが標準偏差である、と考えればよい。この標準偏差で表されたばらつきのことを不確かさ評価においては「標準不確かさ」と呼ぶ。
そして、各標準不確かさを合成すると測定結果のばらつきを標準偏差で表したものが得られる。それを「合成標準不確かさ」と呼ぶ。ここで、合成標準不確かさは測定結果のばらつきの平均値である。しかしこれまで一般的に測定結果のばらつきを表すためには、標準偏差、つまりばらつきの平均値で表すことは多くはなく、ほとんどは値の存在範囲、例えば、(測定結果)±(存在範囲の半幅)のような形で行われる。よって、合成標準不確かさを変換して、存在範囲の半幅を求める。その存在範囲の半幅のことを「拡張不確かさ」と呼ぶ。この拡張不確かさは最終的に報告する不確かさとして用いられており、校正証明書に記載された不確かさも拡張不確かさとなっている。
上記を図示したものを図2に示す。
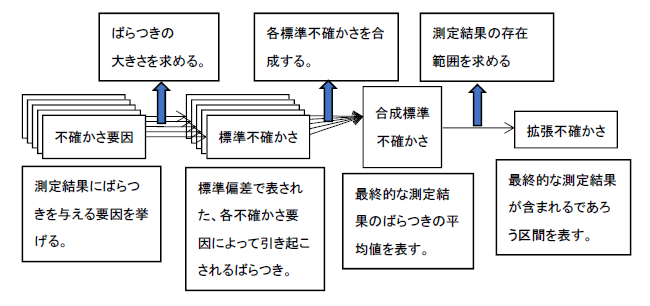
図2:不確かさ算出の流れ
5.最後に
非常に簡単ではあるが、不確かさに関する話題、不確かさの意味、不確かさの算出について解説した。ただし、特に不確かさの算出については簡単な原理だけの紹介であり、実際の算出にはいろいろ考慮すべきことはまだまだたくさん存在する。興味を持った方は筆者が所属する研究グループが運営するWebsite4)を参考にしてほしい。ここには初心者用の解説をはじめとしたさまざまな資料を公開している。ぜひ活用していただきたい。
参考文献
略歴
田中 秀幸 (たなか ひでゆき)
2000年筑波大学大学院工学研究科修了 博士(工学),同年通商産業省 工業技術院 計量研究所 計測システム部 計測数理研究室 研究官,2001年産業技術総合研究所へ改組,現在国立研究開発法人 産業技術総合研究所 計量標準総合センター 物質計測標準研究部門 計量標準基盤研究グループ 主任研究員。
これまで測定の不確かさ評価,試験所間比較に関する研究・普及活動に従事。
|



