日本食品標準成分表は食品の品目別に、可食部100 gあたりの水分、たんぱく質、脂質、炭水化物、灰分などの質量を整理したデータベースである。はんぺんやパンのような多孔質な食品では、空隙の中に空気が入っているが、この成分表には「空気」の項目はない。空気は食品を構成する実質的な成分ではなく、食品の栄養機能や健康にかかわる機能への貢献がないため「成分」と認識されていないことが大きな理由であるが、そもそも空気は質量がほぼゼロであるため、質量基準でまとめられている日本食品標準成分表には載ってこないのである。
　確かに空気の質量は他成分に比べて無視できるほど小さいが、食品の成分構成を体積基準で考えると空気は量的に無視できない成分となる。空隙の存在により、やわらかくなるなど物性に大きく関わっていることも知られている。このように考えると、空気は食品の2次機能に影響を与える重要な「成分」因子であると言うこともできる。食品物性は食品の成分と構造に影響を受けるが故に、食品物性と成分の関係を検討する場合、空気に限らず、その物性を質量ベースで考えるべきか、それとも体積ベースで考えるべきなのかを意識しておく必要がありそうである。
　本稿では、食品物性について考える際に、あまり意識することのない質量基準の物性と体積基準の物性の違いについて述べることとする。

2-1．物質定数と物体定数

食品のかたさに関係するみかけのヤング率は、代表的な物性値である。応力－歪線の傾きで定義され、基本的には物質に固有の物理量であり、試料の形状や大きさには関係しない。このような物理量を物質定数という。一方、食品の弾性を考える際のモデル図によく出てくるばねは、伸び縮み量に比例して抵抗する性質がある。この性質はばね定数（単位はN/m）として表すことができる。同じ鋼材であっても、線径、コイル径、巻き数が異なるとばね定数も異なってくる。伸び縮みに対して抵抗するのは、鋼材という「物質」に固有の性質ではなく、螺旋構造が持つ性質である。このように構造、形状や大きさに影響を受ける性質を表す物質量を物体定数という。
　この物体定数は広義の物性値（工学定数）であるが、モノを特定した議論が必要になるため、本稿では構造や形状による影響がない物質定数を扱うこととする。以降、これを物性定数と称することとする。

2-2．関数と物性

我々は普段から食品を少しつまんだり、つついたりすることで食品のかたさを何気なく判断している。例えば、 図1（a）のように指先で食品をつついたとき、その表面が少し凹む。微小な凹み量を指先が敏感に感じとり、凹み量に関する膨大な記憶と照合することで、かたさを判断している訳である。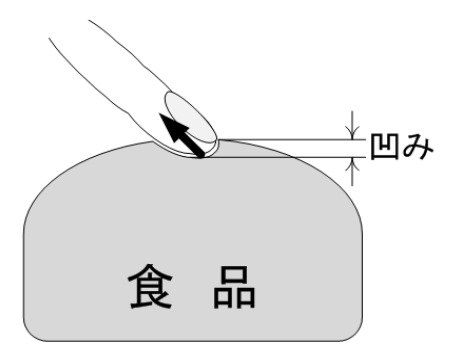
　つつく際の指先の力を大きくすると、凹み量はさらに大きくなる。いま、食品Aと、それよりもかたい食品Bについて、それぞれつついた時の凹み量を変えながら、指先にかかる抵抗力を記録したとする。そのデータをプロットするとおそらく図1（b）に示すグラフが得られるはずである。食品Aと食品Bはどちらも原点を通る1次の直線式 ｙ＝αｘ で近似される。一定の凹み量を与えるために必要な力はかたい食品Bの方が大きいことから、この直線式の傾き α を「かたさ」の指標とすることは合理的な判断と言ってよい。この指による圧縮に代わり平板プランジャーで整形試料を圧縮したときの垂直応力 σ と歪 ε の関係は、図1（c）のように1次の直線式 σ＝Ｅε で表される。この式中の係数 Ｅ がヤング率に相当する。
　直線式 ｙ＝αｘ の ｙ は変数 ｘ の関数 ｆ(ｘ) である。指でつついた時のかたさの指標はこの「関数」の「係数 α 」に相当する。平板プランジャーによる圧縮により得られる直線式 σ＝Ｅε から、垂直応力 σ は歪 ε の関数で表され、この「関数」の「係数」がヤング率 Ｅ に相当する。

図1　食品のかたさの定義
（ａ）食品をつついた時の凹みと指先で感じる力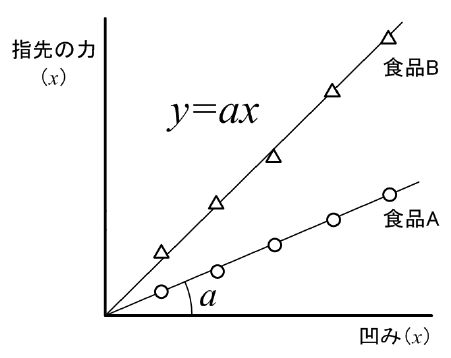


図1　食品のかたさの定義
（ｂ）食品A（やわらかい）と食品B（かたい）をつついた時の凹み量と指先にかかる抵抗力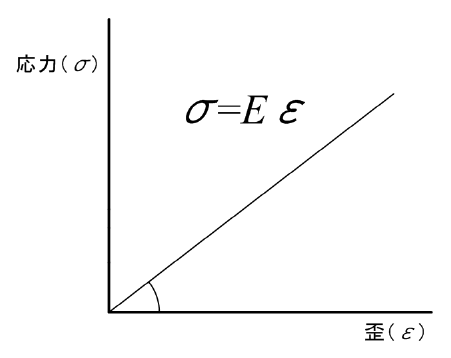


図1　食品のかたさの定義
（ｃ）垂直応力と歪の関係

粘性に関するニュートンの法則は、式（1）で示すようにせん断応力 τ_ｙｘ が速度勾配 ｄｖ_ｘ/ｄｙ に比例する微分方程式で表される。また熱伝導に関するフーリエの法則は、式（2）に示すように、熱流束 Ｑ が温度勾配 ｄＴ/ｄｘ に比例する微分方程式で表される。（ただし、 x と y は空間の座標軸とする。）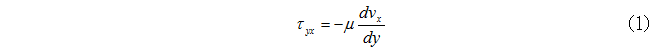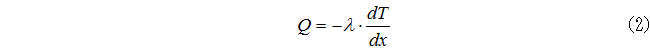

　

これら微分方程式も関数であり、式（1）と（2）の「係数」が粘性係数 μ 、熱伝導率 λ である。
　図1（d）に示すように動的な変位を与えると、得られる反力も動的な応答になる。このような振動的変化は複素量で表すことができる。変位と反力をそれぞれ複素歪 ε^* と複素応力 σ^* で表すと、それらは次式で示すような関係で結ばれる。

これは複素量の関数であり、式（3）の「係数」である複素量 Ｅ^* が複素弾性率、つまり動的弾性率の Ｅ'＋ｉＥ" （ｉ は虚数）である。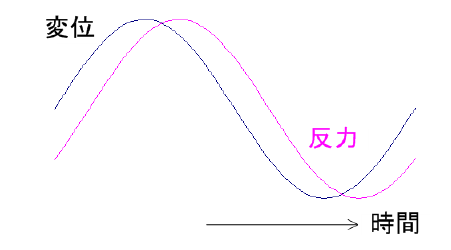
　以上から、物性定数とは、ある系（試料）に何か摂動（入力）を与えた時、その変動分に対して注目する性質の変化（出力）の比（出力÷入力）を示すものと言うことができる。つまり、入力に対する出力の比であり、出力＝物性定数×入力という関数で考えると、物性定数は、「関数式の係数」ということになる。

図1　食品のかたさの定義
（ｄ）動的な変位と反力の関係

2-3．単位から考える質量基準と体積基準

食品の主成分である水について、ハンドブックなどのデータベースに必ず掲載される代表的な物性定数の種類とその単位を表1に示す。

表1　代表的な物性値と単位

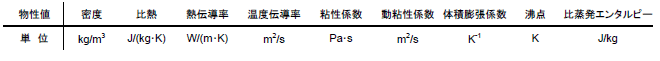
いずれの物性定数も、定義としては本質的に与える摂動は一種類である。その摂動の対象が質量や体積そのものの場合、物性定数の単位の分母はそれぞれkgとm³になる。物性定数の単位の分母から判断すると、表1に挙げる物性定数の中では、例えば比熱や比蒸発エンタルピーは質量あたりの単位を持つ質量基準の物理量（質量または体積あたりの物性定数には「比」という接頭辞がつく）と言うことができる。そういう見方からすると、密度は体積基準ということになる。
　一方、物性定数を定義する関数の中に示量性の物理量が入ってくる系では、対象の質量、体積、大きさ（代表長さ）あたりで考えることがある。また、入力量や出力量の定義がそもそも質量、体積、大きさあたりの量のこともある。表1の中にある熱伝導率は、式（2）に示す通り、温度勾配（単位はK/m）を入力とする関数の係数である。温度勾配は単位空間距離を隔てた地点の温度差のことであるため、熱伝導率は大きさ基準の物性定数と考えるべきである。このことについては後述する。

食品は多成分混合系である。物性に加成性があれば、食品の物性定数は、その構成する成分の物性定数に、その成分の質量割合もしくは体積割合を乗じたものの総和として求めることができる。しかし物性によって成立するものと成立しないものがある。このことについて、質量基準の物性定数と体積基準の物性定数という観点から考察してみる。

3-1．比熱は質量基準の物性

系の温度を1 Kだけ増加させるのに必要な熱量を熱容量（単位はJ/K）と呼ぶ．熱容量は示量性であり、単位質量あたりの熱容量とすることで物質固有の比熱（単位はJ/(kg･K)）になる。食品が脂質、炭水化物、たんぱく質、水の各成分の混合系で、成分間相互作用がなければ比熱に加成則が成立するとしてよい。食品の主成分である水は、その他の成分に比較して含有量が多く、その比熱が4.18 kJ/(kg･K)¹⁾とその他の成分（脂肪1.90 kJ/(kg･K)，炭水化物1.22 kJ/(kg･K)，たんぱく質1.90 kJ/(kg･K)）¹⁾にくらべて2倍以上大きい。従って近似的に水とそれ以外の固形物から構成されている2成分系と考えてよく、Siebelの式のように比熱と水分は1次の線形関係で近似できる²⁾。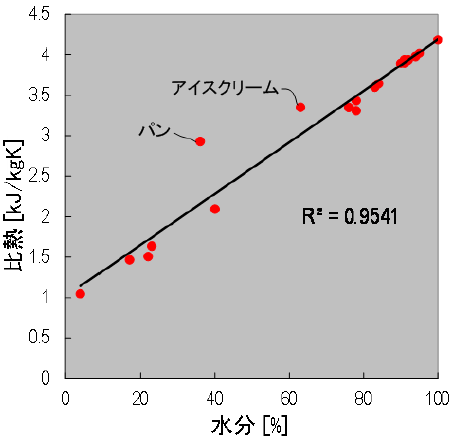
　林 弘通 著の食品物理学（養賢堂，1989）に掲載されている各種食品の水分と比熱の実測データ³⁾を用いてグラフを作成した（図2）。食品の種類を問わず、ほぼ同じ直線近傍にプロットされており、ほぼ2成分系の加成則が成立していると考えてよい。冒頭に述べた内部空隙のある食品のうち、パンとアイスクリームは外れているものの、レタスやキノコなど空隙のある野菜類のプロットが同一直線上にあり、比熱は空隙の影響がないことがわかる。
　ここで、比熱には空気の存在に影響を受けない理由について考えてみる。比熱は単位の分母に質量があることから質量基準の物理量である。空気の密度（約1.2 kg/m³）は、その他の成分（脂肪，炭水化物，たんぱく質）の密度の約1000分の1である。例えば空隙率が25 %（v/v）の食品を考えた場合、空気とその他の成分の密度をそれぞれ1.0 kg/m³、1.0×10³ kg/m³とすると、空気の質量分率は0.03 %となる。比熱に加成則が成立しているとすれば、空気の比熱が、他成分の比熱と同じ大きさであったとしても、みかけの比熱に及ぼす影響は0.03 %しかなく、空気の比熱の関与はほとんどないとみなしてよい。

図2　新鮮な食品の水分と比熱の関係³⁾
（林 弘通 著 食品物理学（養賢堂，1989）pp.103 表3.10に掲載のデータをプロットした）

3-2．熱伝導率は体積基準の物性

式（2）に示すように、系内のある面を単位時間・単位面積あたり通過する熱量である熱流束（J/(m²･s)）は温度勾配（K/m）に比例する。その比例係数が熱伝導率（W/(m･K)）である。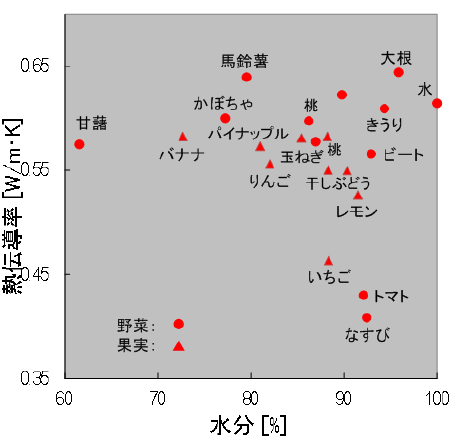
　食品の主成分である水の熱伝導率は0.6 W/(m･K)⁴⁾であり、他成分の熱伝導率（脂肪0.18 W/(m･K)，炭水化物 0.245 W/(m･K)，たんぱく質 0.2 W/(m･K)，空気 0.025 W/(m･K)）⁴⁾は水よりも小さい。よって他成分、とりわけ熱伝導率の小さい脂肪や空気の含有量が高い食品の熱伝導率は減少する傾向にある。
　水の比熱と同様、水の熱伝導率も他の成分よりも大きい。それ故、熱伝導率についても近似的に水とそれ以外の固形物から構成されている2成分系と考えることができるであろうか。空気含有率がほとんど無視できる液状食品では、水分が増すほど熱伝導率も増加し、高水分ほど水の熱伝導率に漸近していく。また両者には線形関係がみられ、固体食品でも肉類、穀物類、乳製品など、比較的空気を含まないものについては、水分と熱伝導率には線形関係がみられるものが多い⁵⁾。以上のことは空気含有率がほとんどない食品にのみ言えることで、ほとんどの食品には空気が含まれるために、一般的には水分と熱伝導率との間に相関を見出すことはできない。図3の果菜類の水分と熱伝導率の関係⁶⁾が示すように、比熱のような線形関係は見られない。果菜類は組織中の細胞間隙にガスを貯えているが、その体積分率は種類によって大きく異なるため、熱伝導率を水分から予測することはできないのである。
　さて、熱伝導率は式（2）から（単位面積あたりの熱量の移動速度）と（空間1 mあたりの温度差）の比であり、その単位は次のように表すことができる。

図3　果菜類の水分と熱伝導率の関係⁶⁾
（林 弘通 著 食品物理学（養賢堂，1989）pp.180 付図7に掲載のグラフを再プロットした）

つまり熱伝導率は「空間（距離）の温度差」が基準の物性定数であり、単位面積あたりのことを考えると体積基準の物性定数と言うこともできる。多孔質食品中の空隙の存在率は、質量分率では前述の通りゼロに等しいが、体積分率では無視できないほど大きい。他成分よりも熱伝導率の低い空気が「空間的」に無視できない量だけ存在すると、みかけの熱伝導率に影響を及ぼす。
　体積基準の物性定数は、本来は体積ベースで加成性を考える必要がある。しかし、各成分の体積分率が同じでも系内での各成分の空間配置が異なると、熱伝導率も異なってくる。そのため、実際の応答に一致するように、各成分の並列モデル、直列モデル、そしてそれらを複雑に組み合わせたモデルが提案されている^7,8)。

食品の物性定数が質量基準か体積基準であるかを意識しなければならないのは、質量はほとんどないに等しいが空間的に無視できない大きさを持つ空気が食品のみかけの物性に及ぼす影響について考える場合にほぼ限定される。その場合、質量基準の物性はおおよそ加成則を満足するが、体積（または大きさ）基準はそうではないと考えておくとよい。もちろん各成分の相互作用により、質量基準であっても加成性を示さない場合があることを付記しておく。

1　 林 弘通：食品物理学，pp.97，養賢堂（1989）

2　 林 弘通：食品物理学，pp.91，養賢堂（1989）

3　 林 弘通：食品物理学，pp.103，養賢堂（1989）

4　 林 弘通：食品物理学，pp.104，養賢堂（1989）

5　 林 弘通：食品物理学，pp.109-110，養賢堂（1989）

6　 林 弘通：食品物理学，pp.180，養賢堂（1989）

7　 西津貴久，近藤 直，林 孝洋，清水 浩，後藤清和，小川雄一 編：農産物性科学1－構造的特性と熱・力学的特性－，pp.96-98，コロナ社（2011）

8　 豊田浄彦，内田敏則，北村豊 編：農産食品プロセス工学，pp.22-23，文永堂出版（2015）

西津　貴久（ニシヅ　タカヒサ）
岐阜大学　応用生物科学部　応用生命科学課程　教授

【略歴】
1990年3月　京都大学大学院農学研究科修士課程　中途退学
1990年4月　京都大学農学部　助手
2008年4月　岐阜大学応用生物科学部　准教授
2014年3月　岐阜大学応用生物科学部　教授
現在に至る