人の感覚を使って物の特性を評価することを官能評価と呼んでいる。ここでは、官能評価の代表的な試験方法を紹介する。

1.1　官能評価試験のタイプ
　 人の感覚器官を使って、試料の差異を評価すること、あるいは、差異を検出する能力の有無を調査することを目的とした官能評価を分析型官能評価と呼ぶ。一方、人はどのような試料を好むのかを調査することを目的とした官能評価を嗜好型官能評価という。

1.2　分析型試験の方法
　 官能評価において使われる分析型試験の代表的な方法を紹介する。

■2点識別法　
　2つの試料AとBをパネルに提示し、どちらが刺激（特性）をより強く感じるかを評価させる方法を2点識別法という。AとBは刺激の強さの異なる試料を与えるため、刺激の強いのはA（あるいはB）であるというように正解が存在する。この方法は評価者に識別能力（違いを見分ける能力）があるかどうか、あるいは、2つの試料に差異があるかどうかを調査するときに用いる試験方法である。
　評価者の識別能力を調べるときには、「1人の評価者にn回」実施する。または、２つの試料間に差異があるかどうかを調べるときには、「n人の評価者に1回ずつ（あるいは２回以上）」実施される。
　試験の結果は、正解した回数や人数によって、識別能力の有無や差異の有無を統計学的に判定する。
■1対2点識別法　
　2つの試料AとBを識別するのに、AまたはBを1つ標準品Sとして提示して、別にAとBを提示して、どちらがSと同じかを当てさせる方法である。
　2点識別法と同様に、パネルに識別能力（違いを見分ける能力）があるかどうか、あるいは、2つの試料間に差異があるかどうかを調査するときに用いる方法である。この試験方法は、あらかじめ、着目する差異を特定できないような試料の識別に用いられる。
■3点識別法
　2つの試料を識別するために、どちらか一方を2個、他方を1個、合計3個をパネルに提示して、異なる1個を当てさせる方法である。
　組合せの作り方には、次の2つの方法がある。
　　（1） （　A　・　A　・　B　）※　Bを当てさせる
　　（2） （　A　・　B　・　B　）※　Aを当てさせる

■1点識別法（A非A識別法）
　2つの試料Aと非A（B）の一方だけをランダムな順序でパネルに提示して、AかAでないかを回答させる方法を1点識別法という。
■2対5点識別法
　2種類にコード化された5つの試料を、2個と3個のグループに分ける試験方法を2対5点識別法という。たとえば、2種類の清酒AとBについて、2個のAと3個のBの合計5個をランダムな順序でパネルに提示して、どの2個がAであるか（どの3個がBであるか）を判断させる。

1.3　嗜好型試験の方法
　 官能評価において使われる嗜好型試験の代表的な方法を紹介する。

■2点嗜好法
　2つの試料AとBをパネル（人）に提示し、どちらが好ましく感じるかを評価させる方法を2点嗜好法という。人はどのような試料を好むかという嗜好を調査するときに用いる方法である。この方法はn人のパネルに実施して、どちらのほうを好むパネルが多いかを統計的に判定する。
■選択法
　異なるt個の試料を提示して、パネルに最も好きな試料（あるいは、最も好ましくない試料）を選ばせる方法を選択法という。
■順位法
　異なるt個の試料を提示して、パネルの好きな順に1位からt位まで順位をつけさせる方法を順位法という。
■採点法
　試料の特性を何段階かで点数化してデータを収集する方法を採点法という。
[採点法（5段階評価）の例 ]　
　1　おいしい
　2　どちらかといえばおいしい
　3　どちらともいえない
　4　どちらかといえばまずい
　5　まずい

■一対比較法
　異なるt個の試料から2つずつ取り上げて組をつくり、組ごとに2つの試料を比較しながら評価する方法を一対比較法という。官能試験では、試料の種類が多くなると、同時に評価をするのが困難になるので、2つずつ取り上げて比較する方法が有効になることがある。
　 一対比較法には、2つを比較したときの優劣だけを問う方法（サーストンの方法、ブラッドレーの方法）と、差の程度を問う方法（シェッフェの方法、シェッフェの変法）がある。

官能評価によって得られたデータは統計的に解析する必要がある。このための方法として、よく使われる有効な手法には、次のようなものがあげられる。
　(1)　二項検定
　(2)　χ²検定（カイ2乗検定）
　(3)　ｔ検定
　(4)　分散分析
　(5)　回帰分析
　(6)　判別分析
　(7)　主成分分析
　(8)　対応分析
　(9)　ノンパラメトリック検定
　ここでは、最も基本的な二項検定を取り上げて、統計的な考え方を解説する。

2.1　2点嗜好法の統計解析
　50人の評価者に食品AとBを試食してもらい、どちらがおいしいと感じるかを回答させる実験を行ったとする。結果は30人がA、20人がBと答えた。この結果をグラフに表すと次のようになる。

　

この結果から、統計解析を行わずに、AのほうがBよりも好まれていると判断してはいけない。なぜならば、この結果は50人の結果に過ぎない、また、この程度の差は誤差の範囲かもしれないからである。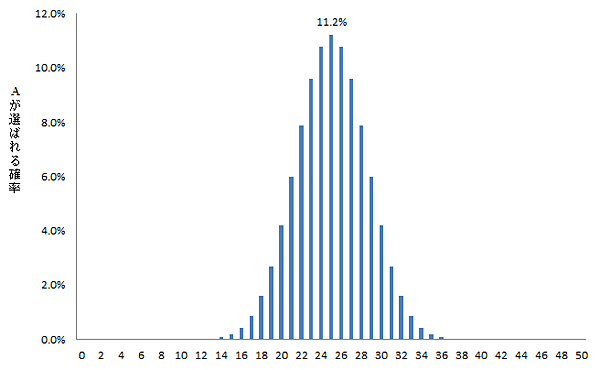
　このような問題に遭遇したときに使う統計解析の方法が二項検定である。まずは、二項検定の方法の前に考え方を述べよう。

■二項分布
　いま、Aが選ばれる確率を0.5、Bが選べられる確率を0.5とする。すなわち、AとBには差がないものとする。このとき、50人の評評価者のうち、Aを選ぶ人がm人である確率を計算してグラフに表現すると、次のようなグラフが得られる。このような分布を二項分布という。

　
　このグラフは縦軸を確率、横軸をm（Aを選ぶ人数）としている。グラフを見ると、試験を50人に実施した場合、Aを選ぶ人数は25人（Bも25人）となるときの確率が最も大きく、その値は11.2％と計算されていることがわかる。25人である確率が最も大きくなるということは、50×0.5＝25という計算をすることで、直感的にも納得できよう。同時に、Ａを選ぶ人数が36人以上になる、あるいは14人以下になる確率は、ほとんど0であり、めったに起きない現象であるということもわかる。


■統計的な考え方と検定
　統計学の世界では、めったに起きない現象と考える確率を0.05以下と考えようというのが慣例的なルールである。この0.05という数値を「有意水準」と呼んでいる。めったに起きないと判断されるときに、「有意である」という言い方をする。
　さて、めったに起きないと判断された、すなわち、有意であると判断されたならば、どのように考えればよいだろうか？それはAが選ばれる確率を0.5と仮定したのが誤りであったと考えるのである。このことは、Aのほうが選ばれやすい、あるいは、Aのほうが選ばれにくい（＝Bのほうが選ばれやすい）と判定することと同じである。このような考え方で、AとBの選ばれやすさが同じかどうかを確認する統計的な方法を検定という。

■二項検定の実施
　さて、50人に「Aを好きか、Bを好きか」を答えてもらう2点嗜好法を実施した場合、どのような結果が得られたときに「有意である」となるかを考えることにしよう。
今回の例では、Aを好きな人が30人、Bを好きな人が20人であった。そこで、母集団（調査の対象とする集団）においては、Aが好きな人とBが好きな人の割合には差がない（Aが好きな人の割合＝0.5）と仮定して、50人中30人以上がAを好きと回答する確率と、その反対に20人以下が好きと回答する確率を計算する。このような計算はExcelで簡単に計算することができる。計算式は次のようになる。

　20人以下が好きと回答する確率　　=BINOM.DIST(20,50,0.5,1)　　＝0.1013
　30人以上が好きと回答する確率　　=1−BINOM.DIST(29,50,0.5,1)　＝0.1013

以上の計算結果から、50人中30人以上がAを好きと回答する確率と、その反対に20人以下が好きと回答する確率を合計すると、0.1013＋0.1013＝0.2026となり、有意水準の0.05よりも大きい。したがって、有意でない、すなわち、AとBには差があるとはいえないと判断することになる。
　この例における確率の値（0.2026）を検定のp値と呼んでいる。検定においては、このp値が最も重要である。検定ではp値を計算して、次のような規則で差があるかないかを判断することにしている。

p値≦0.05　ならば　有意である　→　差があるといえる
　p値＞0.05　ならば　有意でない　→　差があるといえない

2.2　2点識別法の統計解析
　60人の評価者にアルコール飲料AとBを試飲してもらい、どちらのアルコール濃度が強いかを回答させる実験を行ったとする。ここでAのほうがBよりも濃度を強くしている。したがって、Aと回答するのが正解である。回答結果は40人がA、20人がBと答えた。この結果から、AとBには識別できるだけの差があるといえるかを先の二項検定を使って、判定してみよう。2点嗜好法のときの真似をするならば、次のような計算を行うことになる。

20人以下がAと回答する確率　　=BINOM.DIST(20,60,0.5,1)　　＝0.00674
　40人以上がAと回答する確率　　=1−BINOM.DIST(39,60,0.5,1)　＝0.00674

2点嗜好法のときには、この2つの確率を合計してp値とした。しかし、2点識別法の場合は、A（正解）と回答するほうを最初から期待しているので、20人以下がAと回答する確率は求めなくてよいのである。したがって、この場合のp値は0.00674となる。

p値＝0.00674　＜　0.05　なので、有意である。
　 すなわち、AとBには識別できる差があるといえる。

2点識別法のように、一方の方向だけを問題にする検定を片側検定と呼び、2点嗜好法のように両方向を問題にする検定を両側検定と呼んでいる。

 

★　次号では、順位データの解析方法を中心に統計解析の事例について解説する。

内田　治（うちだ　おさむ）
東京理科大学大学院修士課程終了
現職
東京情報大学総合情報学部　准教授
著書
JMPによるデータ分析（東京図書）
すぐに使えるExcelによるアンケートの集計と解析（東京図書）
ビジュアル　品質管理の基本（日本経済新聞社）
ほか